Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of the following expression and round to the nearest integer: sum_(n=1)^(62)40(1.03)^(n) Answer:

Find the value of the following expression and round to the nearest integer:\newline∑n=16240(1.03)n \sum_{n=1}^{62} 40(1.03)^{n} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

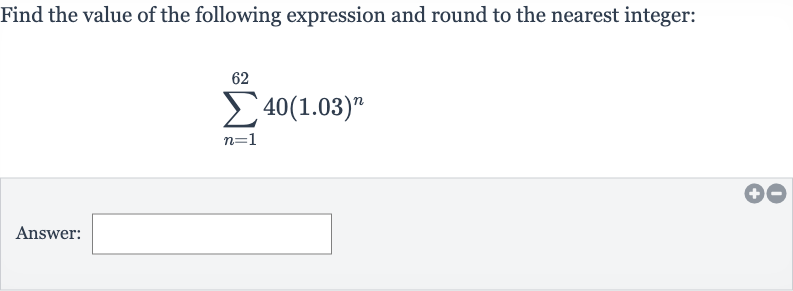
Q. Find the value of the following expression and round to the nearest integer:\newline∑n=16240(1.03)n \sum_{n=1}^{62} 40(1.03)^{n} \newlineAnswer:
  1. Given Series Information: We are given a geometric series with the first term a=40(1.03)1a = 40(1.03)^1 and the common ratio r=1.03r = 1.03. The sum of the first nn terms of a geometric series is given by the formula Sn=a(1−rn)(1−r)S_n = \frac{a(1 - r^n)}{(1 - r)}, where nn is the number of terms. We need to find the sum of 6262 terms.
  2. Calculate First Term: First, let's calculate the first term of the series: a=40(1.03)1=40×1.03a = 40(1.03)^1 = 40 \times 1.03.
  3. Calculate Common Ratio: Now, we calculate the common ratio rr, which is 1.031.03. Since it is greater than 11, the series is increasing.
  4. Calculate 6262nd Term: Next, we calculate the 62nd62^{\text{nd}} term of the series using the formula for the nthn^{\text{th}} term of a geometric series, which is an=a⋅r(n−1)a_n = a \cdot r^{(n-1)}. So, a62=40⋅1.03(62−1)=40⋅1.0361a_{62} = 40 \cdot 1.03^{(62-1)} = 40 \cdot 1.03^{61}.
  5. Use Sum Formula: Now we can use the sum formula for a geometric series: S62=a(1−r62)/(1−r)S_{62} = a(1 - r^{62}) / (1 - r). Plugging in the values we have S62=40×1.03(1−1.0362)/(1−1.03)S_{62} = 40 \times 1.03(1 - 1.03^{62}) / (1 - 1.03).
  6. Perform Calculations: We perform the calculations for the sum: S62=40×1.03(1−1.0362)/(1−1.03)=40×1.03(1−1.0362)/(−0.03)S_{62} = 40 \times 1.03(1 - 1.03^{62}) / (1 - 1.03) = 40 \times 1.03(1 - 1.03^{62}) / (-0.03).
  7. Calculate Exponentiation: We need to calculate 1.03621.03^{62}. This is a large exponentiation, and it's best to use a calculator for this step to avoid any math errors.
  8. Substitute Value: After calculating 1.03621.03^{62}, we substitute this value back into the sum formula to get the exact value of the sum.
  9. Round to Nearest Integer: Finally, we round the result to the nearest integer as the question prompt asks for the value rounded to the nearest integer.

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant