Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of the following expression and round to the nearest integer: sum_(n=2)^(22)40(1.2)^(n-1) Answer:

Find the value of the following expression and round to the nearest integer:\newline∑n=22240(1.2)n−1 \sum_{n=2}^{22} 40(1.2)^{n-1} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

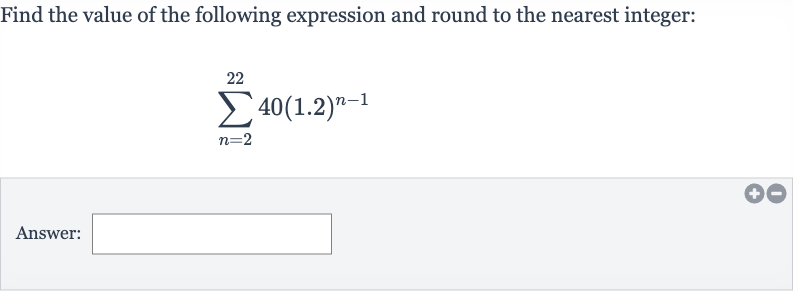
Q. Find the value of the following expression and round to the nearest integer:\newline∑n=22240(1.2)n−1 \sum_{n=2}^{22} 40(1.2)^{n-1} \newlineAnswer:
  1. Recognize as geometric series: Recognize the sum as a geometric series. The general form of a geometric series is ∑n=0∞arn\sum_{n=0}^{\infty} ar^n, where aa is the first term and rr is the common ratio. In this case, a=40(1.2)2−1=40(1.2)a = 40(1.2)^{2-1} = 40(1.2) and r=1.2r = 1.2.
  2. Calculate first term: Calculate the first term of the series.\newlineThe first term is when n=2n=2, so we have a=40(1.2)2−1=40(1.2)=48a = 40(1.2)^{2-1} = 40(1.2) = 48.
  3. Use formula for sum: Use the formula for the sum of a finite geometric series.\newlineThe sum of the first kk terms of a geometric series is given by Sk=a(1−rk)(1−r)S_k = \frac{a(1 - r^k)}{(1 - r)}, where kk is the number of terms. Here, k=22−2+1=21k = 22 - 2 + 1 = 21 terms.
  4. Calculate sum: Calculate the sum of the series.\newlineUsing the formula from Step 33, we have S21=48(1−1.221)/(1−1.2)S_{21} = 48(1 - 1.2^{21}) / (1 - 1.2).
  5. Perform calculations: Perform the calculations.\newlineS21=48(1−1.221)1−1.2=48(1−1.221)−0.2=−240(1−1.221)S_{21} = \frac{48(1 - 1.2^{21})}{1 - 1.2} = \frac{48(1 - 1.2^{21})}{-0.2} = -240(1 - 1.2^{21}).
  6. Calculate exact value: Calculate the exact value of 1.2211.2^{21}. 1.2211.2^{21} is approximately 109.41898913151242109.41898913151242 (using a calculator).
  7. Substitute value into sum: Substitute the value from Step 66 into the sum.\newlineS21=−240(1−109.41898913151242)=−240(−108.41898913151242)=26020.55747150297S_{21} = -240(1 - 109.41898913151242) = -240(-108.41898913151242) = 26020.55747150297.
  8. Round to nearest integer: Round the result to the nearest integer.\newlineThe sum rounded to the nearest integer is approximately 2602126021.

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant