Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of the following expression and round to the nearest integer: sum_(n=1)^(86)20(1.02)^(n) Answer:

Find the value of the following expression and round to the nearest integer:\newline∑n=18620(1.02)n \sum_{n=1}^{86} 20(1.02)^{n} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

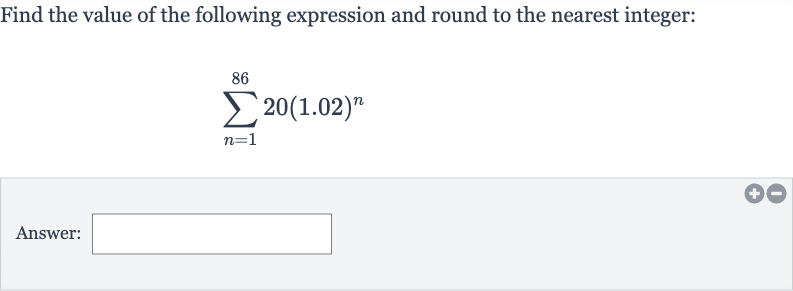
Q. Find the value of the following expression and round to the nearest integer:\newline∑n=18620(1.02)n \sum_{n=1}^{86} 20(1.02)^{n} \newlineAnswer:
  1. Recognize as geometric series: Recognize the sum as a geometric series.\newlineThe general form of a geometric series is ∑n=0Narn\sum_{n=0}^{N} ar^n, where aa is the first term, rr is the common ratio, and NN is the number of terms.\newlineIn this case, a=20(1.02)a = 20(1.02), r=1.02r = 1.02, and N=86N = 86.
  2. Use formula for sum: Use the formula for the sum of a finite geometric series.\newlineThe sum SS of the first NN terms of a geometric series is given by S=a(1−rN)/(1−r)S = a(1 - r^N) / (1 - r), provided that |r| < 1.\newlineHere, we need to adjust the formula because our series starts at n=1n=1, so we subtract the first term (n=0n=0) from the sum.
  3. Calculate sum using formula: Calculate the sum using the adjusted formula.\newlineS=20(1.02)(1−(1.02)86)/(1−1.02)−20(1.02)0S = 20(1.02)(1 - (1.02)^{86}) / (1 - 1.02) - 20(1.02)^0\newlineSince (1.02)0=1(1.02)^0 = 1, we subtract 2020 from the sum.\newlineS=20(1.02)(1−(1.02)86)/(−0.02)−20S = 20(1.02)(1 - (1.02)^{86}) / (-0.02) - 20
  4. Perform calculations: Perform the calculations.\newlineS=20(1.02)(1−(1.02)86)/(−0.02)−20S = 20(1.02)(1 - (1.02)^{86}) / (-0.02) - 20\newlineS=−20(1.02)(1−(1.02)86)/0.02−20S = -20(1.02)(1 - (1.02)^{86}) / 0.02 - 20\newlineS=−20(1.02)(1−(1.02)86)×50−20S = -20(1.02)(1 - (1.02)^{86}) \times 50 - 20\newlineS=−20×50×(1.02−(1.02)87)−20S = -20 \times 50 \times (1.02 - (1.02)^{87}) - 20\newlineS=−1000×(1.02−(1.02)87)−20S = -1000 \times (1.02 - (1.02)^{87}) - 20
  5. Calculate power of 1.02871.02^{87}: Calculate the power of 1.02871.02^{87}. This step involves using a calculator or a computer to find the value of (1.02)87(1.02)^{87}.
  6. Substitute value of 1.02871.02^{87}: Substitute the value of (1.02)87(1.02)^{87} into the sum.\newlineAssuming the value of (1.02)87(1.02)^{87} is calculated correctly, substitute it back into the expression for SS.\newlineS=−1000×(1.02−(1.02)87)−20S = -1000 \times (1.02 - (1.02)^{87}) - 20
  7. Complete calculation and round: Complete the calculation and round to the nearest integer.\newlineAfter finding the exact value of SS, round it to the nearest integer to get the final answer.

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant