Full solution
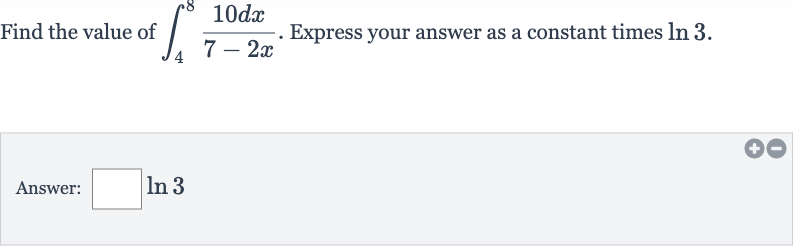
Q. Find the value of . Express your answer as a constant times .Answer:
- Identify the integral: Identify the integral to be solved.We need to evaluate the integral of the function from to .
- Simplify the integral: Simplify the integral.Let's use a substitution method to simplify the integral. We can let , which means or .
- Change limits of integration: Change the limits of integration. When , . When , . So the new limits of integration are from to .
- Rewrite integral in terms of u: Rewrite the integral in terms of u.The integral becomes:.
- Evaluate the integral: Evaluate the integral.The integral of is . So we have: from to .
- Apply limits of integration: Apply the limits of integration. .Since , it simplifies to .
- Simplify the expression: Simplify the expression.We know that is the same as , so the integral simplifies to:.
- Express answer as constant times : Express the answer as a constant times . The final answer is .