AI tutor
Full solution
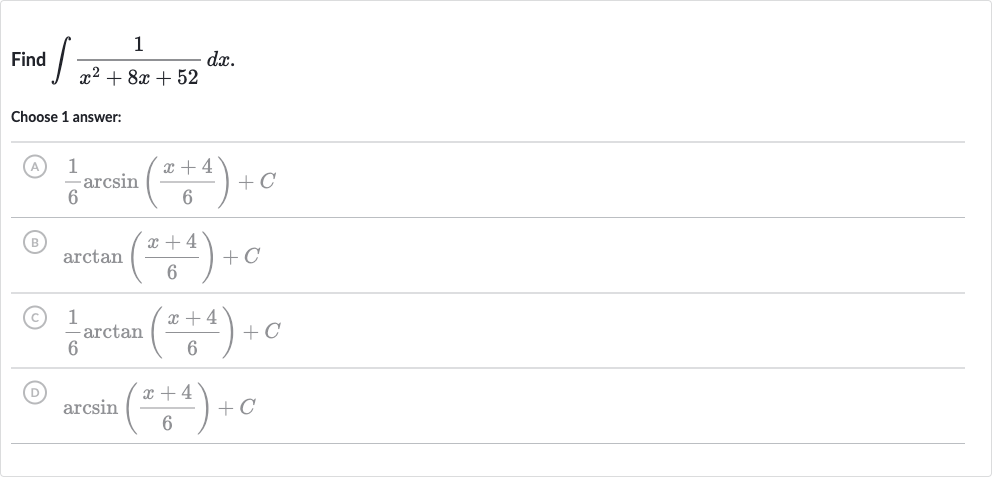
Q. Find .Choose answer:(A) (B) (C) (D)
- Rewrite with completed square: Rewrite the integral with the completed square..
- Recognize inverse tangent form: Recognize the integral as a form of the inverse tangent function.The integral of is .Here, and .
- Calculate using inverse tangent formula: Calculate the integral using the formula for the inverse tangent. .