Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

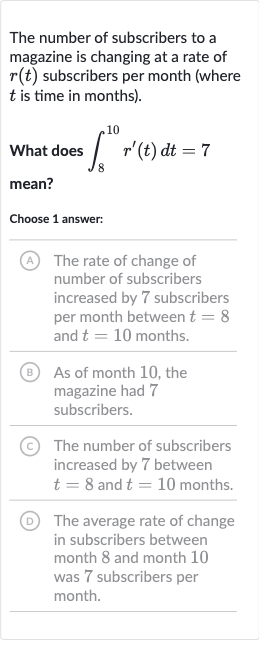
The number of subscribers to a magazine is changing at a rate of r(t) subscribers per month (where t is time in months). What does int_(8)^(10)r^(')(t)dt=7 mean? Choose 1 answer: (A) The rate of change of number of subscribers increased by 7 subscribers per month between t=8 and t=10 months. (B) As of month 10, the magazine had 7 subscribers. (C) The number of subscribers increased by 7 between t=8 and t=10 months. (D) The average rate of change in subscribers between month 8 and month 10 was 7 subscribers per month.

The number of subscribers to a magazine is changing at a rate of r(t) r(t) subscribers per month (where t t is time in months).\newlineWhat does ∫810r′(t)dt=7 \int_{8}^{10} r^{\prime}(t) d t=7 mean?\newlineChoose 11 answer:\newline(A) The rate of change of number of subscribers increased by 77 subscribers per month between t=8 t=8 and t=10 t=10 months.\newline(B) As of month 1010, the magazine had 77 subscribers.\newline(C) The number of subscribers increased by 77 between t=8 t=8 and t=10 t=10 months.\newline(D) The average rate of change in subscribers between month 88 and month 1010 was 77 subscribers per month.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the power ruleright chevron icon

Full solution

Q. The number of subscribers to a magazine is changing at a rate of r(t) r(t) subscribers per month (where t t is time in months).\newlineWhat does ∫810r′(t)dt=7 \int_{8}^{10} r^{\prime}(t) d t=7 mean?\newlineChoose 11 answer:\newline(A) The rate of change of number of subscribers increased by 77 subscribers per month between t=8 t=8 and t=10 t=10 months.\newline(B) As of month 1010, the magazine had 77 subscribers.\newline(C) The number of subscribers increased by 77 between t=8 t=8 and t=10 t=10 months.\newline(D) The average rate of change in subscribers between month 88 and month 1010 was 77 subscribers per month.
  1. Interpretation of Integral: The integral of a rate of change function over an interval gives the net change over that interval. In this case, the integral of r′(t)r'(t) from t=8t=8 to t=10t=10 represents the net change in the number of subscribers from month 88 to month 1010.
  2. Calculation of Net Change: Since the integral of r′(t)r'(t) from 88 to 1010 is equal to 77, this means that the total change in the number of subscribers over this time period is 77 subscribers.
  3. Evaluation of Answer Choices: We can now evaluate the answer choices based on the interpretation of the integral:\newline(A) This choice suggests that the rate of change increased, which is not what the integral measures.\newline(B) This choice suggests a total number of subscribers at a specific time, which is not what the integral measures.\newline(C) This choice correctly interprets the integral as the net increase in the number of subscribers over the time interval.\newline(D) This choice suggests an average rate of change, which is not what the integral measures.
  4. Correct Answer Explanation: Based on the above reasoning, the correct answer is (C) The number of subscribers increased by 77 between t=8t=8 and t=10t=10 months.

More problems from Evaluate definite integrals using the power rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(B) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(C) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 9 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(B) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(C) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x \newline(D) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x
Get tutor helpright-arrow

Posted 9 months ago

Question
(1×((12)n−1))/((12)−1)\left(1\times\left(\left(\frac{1}{2}\right)^n-1\right)\right)\bigg/\left(\left(\frac{1}{2}\right)-1\right)
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve∫1(x−2)(x2+x+1) dx\int \frac{1}{(x-2)(x^{2}+x+1)}\,dx.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function f(x)=sin⁡(2x) f(x) = \sin(2x) ?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2}\sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+C \frac{1}{2}\sin(2x) + C
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function  f(x)=sin(2x)\ f(x) = sin(2x)?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2} \sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+c \frac{1}{2} \sin(2x) + c
Get tutor helpright-arrow

Posted 8 months ago

Question
Suppose ∫24f(2x) dx=10 \int_{2}^{4} f(2x) \, dx = 10 . Then ∫48f(u) du= \int_{4}^{8} f(u) \, du =
Get tutor helpright-arrow

Posted 8 months ago

Question
Find ddt∫2t4ex2dx\frac{d}{dt}\int_{2}^{t^{4}}e^{x^{2}}dx
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate and write the answer in scientific notation: \newline(1.48×103)(7×104)÷8.2×1012(1.48\times10^{3})(7\times10^{4})\div8.2\times10^{12}
Get tutor helpright-arrow

Posted 8 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 1 month ago

View all (25)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant