Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

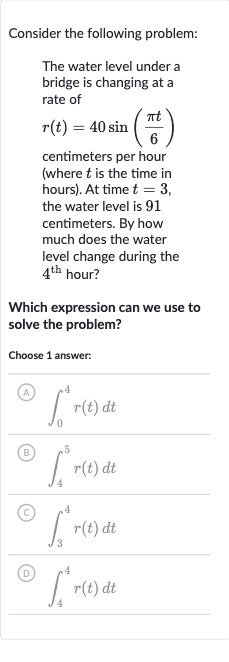
Consider the following problem: The water level under a bridge is changing at a rate of r(t)=40 sin((pi t)/(6)) centimeters per hour (where t is the time in hours). At time t=3, the water level is 91 centimeters. By how much does the water level change during the 4^("th ") hour? Which expression can we use to solve the problem? Choose 1 answer: (A) int_(0)^(4)r(t)dt (B) int_(4)^(5)r(t)dt (C) int_(3)^(4)r(t)dt (D) int_(4)^(4)r(t)dt

Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(B) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(C) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the power ruleright chevron icon

Full solution

Q. Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(B) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(C) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
  1. Define Time Interval: To find the change in water level during the 4th4^{\text{th}} hour, we need to evaluate the rate of change function r(t)r(t) from the start to the end of the 4th4^{\text{th}} hour. The 4th4^{\text{th}} hour starts at t=3t=3 and ends at t=4t=4.
  2. Use Integral Expression: The correct expression to use for this problem is the integral of r(t)r(t) from t=3t=3 to t=4t=4, which represents the total change in water level during the 4th4^{\text{th}} hour. This corresponds to option (C) ∫34r(t) dt\int_{3}^{4}r(t)\,dt.
  3. Calculate Integral: Now we will calculate the integral of r(t)r(t) from t=3t=3 to t=4t=4. ∫3440sin⁡(πt6)dt\int_{3}^{4}40 \sin\left(\frac{\pi t}{6}\right) dt
  4. Apply Antiderivative Rule: To integrate, we use the antiderivative of sin⁡(kx)\sin(kx), which is −1kcos⁡(kx)-\frac{1}{k} \cos(kx), where kk is a constant. In this case, k=π6k = \frac{\pi}{6}.∫3440sin⁡(πt6)dt=−40π/6[cos⁡(πt6)]\int_{3}^{4}40 \sin\left(\frac{\pi t}{6}\right) dt = -\frac{40}{\pi/6} \left[\cos\left(\frac{\pi t}{6}\right)\right] | from t=3t=3 to t=4t=4
  5. Simplify Constant Factor: Simplify the constant factor in front of the integral. \newline−40π/6=−240π-\frac{40}{\pi/6} = -\frac{240}{\pi}\newlineNow we have:\newline−240π[cos⁡(πt6)]-\frac{240}{\pi} [\cos(\frac{\pi t}{6})] | from t=3t=3 to t=4t=4
  6. Evaluate Antiderivative: Evaluate the antiderivative at the upper and lower limits of the integral. \newline−240π[cos⁡(π⋅46)−cos⁡(π⋅36)]-\frac{240}{\pi} [\cos(\frac{\pi \cdot 4}{6}) - \cos(\frac{\pi \cdot 3}{6})]
  7. Calculate Cosine Values: Calculate the cosine values.\newlinecos⁡(π⋅46)=cos⁡(2π3)=−12\cos\left(\frac{\pi \cdot 4}{6}\right) = \cos\left(\frac{2\pi}{3}\right) = -\frac{1}{2} (since cos⁡(2π3)\cos\left(\frac{2\pi}{3}\right) is in the second quadrant where cosine is negative)\newlinecos⁡(π⋅36)=cos⁡(π2)=0\cos\left(\frac{\pi \cdot 3}{6}\right) = \cos\left(\frac{\pi}{2}\right) = 0 (since cos⁡(π2)\cos\left(\frac{\pi}{2}\right) is the cosine of 9090 degrees, which is 00)
  8. Substitute Values: Substitute the cosine values into the expression.\newline−240π[−12−0]=240π×12-\frac{240}{\pi} \left[-\frac{1}{2} - 0\right] = \frac{240}{\pi} \times \frac{1}{2}
  9. Simplify Expression: Simplify the expression to find the change in water level during the 4th4^{\text{th}} hour.240π×12=120π\frac{240}{\pi} \times \frac{1}{2} = \frac{120}{\pi} centimeters

More problems from Evaluate definite integrals using the power rule

Question
The number of subscribers to a magazine is changing at a rate of r(t) r(t) subscribers per month (where t t is time in months).\newlineWhat does ∫810r′(t)dt=7 \int_{8}^{10} r^{\prime}(t) d t=7 mean?\newlineChoose 11 answer:\newline(A) The rate of change of number of subscribers increased by 77 subscribers per month between t=8 t=8 and t=10 t=10 months.\newline(B) As of month 1010, the magazine had 77 subscribers.\newline(C) The number of subscribers increased by 77 between t=8 t=8 and t=10 t=10 months.\newline(D) The average rate of change in subscribers between month 88 and month 1010 was 77 subscribers per month.
Get tutor helpright-arrow

Posted 9 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(B) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(C) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x \newline(D) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x
Get tutor helpright-arrow

Posted 9 months ago

Question
(1×((12)n−1))/((12)−1)\left(1\times\left(\left(\frac{1}{2}\right)^n-1\right)\right)\bigg/\left(\left(\frac{1}{2}\right)-1\right)
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve∫1(x−2)(x2+x+1) dx\int \frac{1}{(x-2)(x^{2}+x+1)}\,dx.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function f(x)=sin⁡(2x) f(x) = \sin(2x) ?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2}\sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+C \frac{1}{2}\sin(2x) + C
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function  f(x)=sin(2x)\ f(x) = sin(2x)?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2} \sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+c \frac{1}{2} \sin(2x) + c
Get tutor helpright-arrow

Posted 8 months ago

Question
Suppose ∫24f(2x) dx=10 \int_{2}^{4} f(2x) \, dx = 10 . Then ∫48f(u) du= \int_{4}^{8} f(u) \, du =
Get tutor helpright-arrow

Posted 8 months ago

Question
Find ddt∫2t4ex2dx\frac{d}{dt}\int_{2}^{t^{4}}e^{x^{2}}dx
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate and write the answer in scientific notation: \newline(1.48×103)(7×104)÷8.2×1012(1.48\times10^{3})(7\times10^{4})\div8.2\times10^{12}
Get tutor helpright-arrow

Posted 8 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 1 month ago

View all (25)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant