AI tutor
Full solution
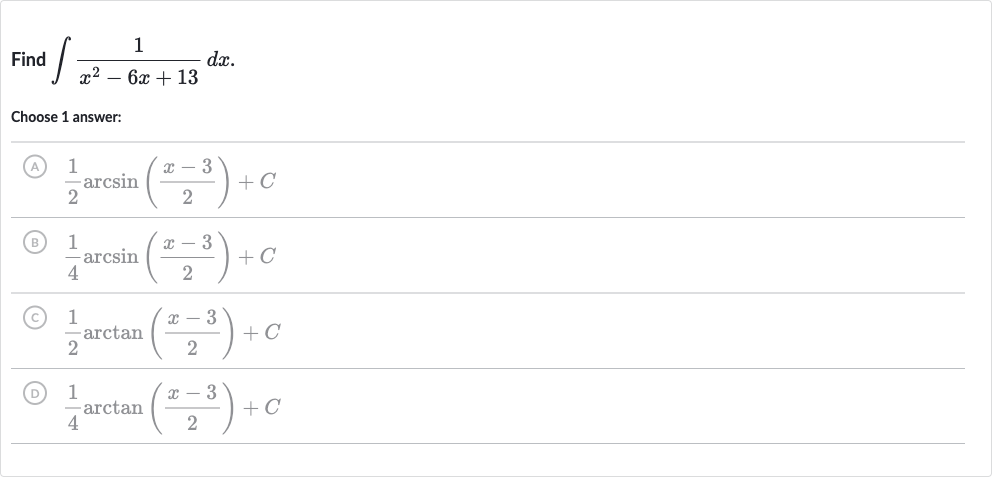
Q. Find .Choose answer:(A) (B) (C) (D)
- Rewrite denominator: Rewrite the denominator as a complete square: .
- Integral form: Now the integral looks like .
- Recognize arctan derivative: Recognize the integral as a form of arctan derivative: .
- Substitute values: Here, , so , and .
- Apply arctan formula: Substitute and into the arctan formula: .
- Match with answer: Match the result with the answer choices: (C) is the correct one.