AI tutor
Full solution
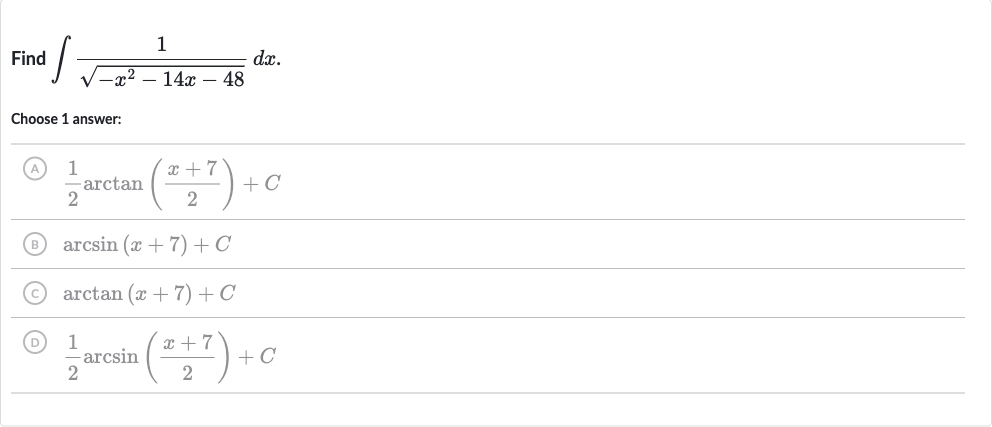
Q. Find .Choose answer:(A) (B) (C) (D)
- Complete the square: First, let's complete the square for the expression under the square root to make it look like a standard integral form.
- Substitute : Now, let's substitute , then . So, the integral becomes .
- Standard integral form: This is a standard integral form that resembles the inverse sine function, . So, the integral becomes .
- Substitute back : Substitute back to get the final answer.
- Match with options: Now, let's match our answer with the given options.The correct answer is .