AI tutor
Full solution
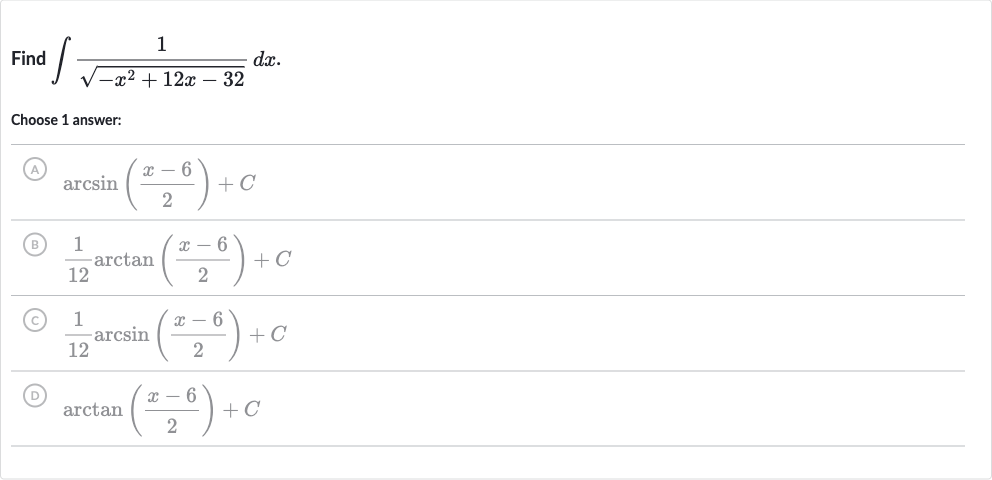
Q. Find .Choose answer:(A) (B) (C) (D)
- Substitute : Now, let's substitute , which means or . The integral becomes .
- Simplify integral: Simplify the integral to get . Recognize that this is the integral form of , since the derivative of is .
- Recognize integral form: Now, integrate to get .
- Integrate to get: Substitute back for to get . But wait, there's a mistake here. The integral should be without the in front, since we already accounted for the substitution.