AI tutor
Full solution
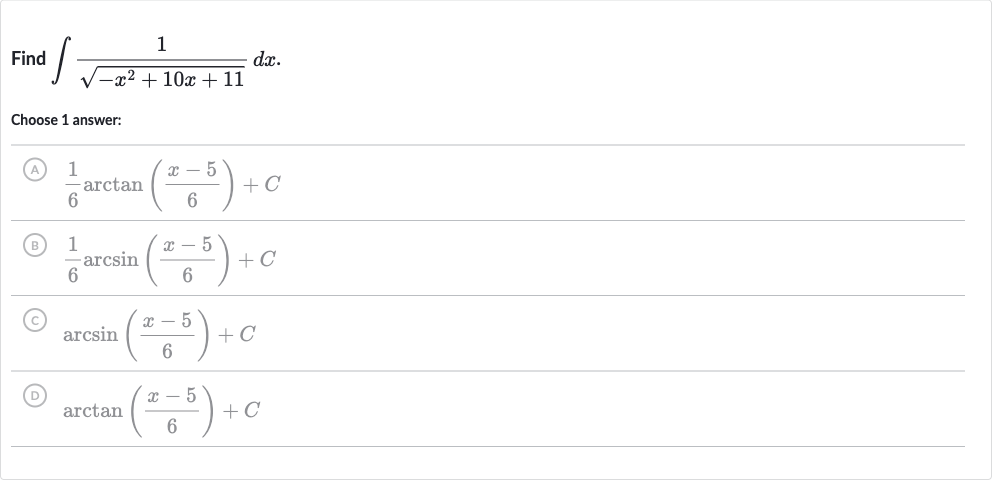
Q. Find .Choose answer:(A) (B) (C) (D)
- Recognize Integral Form: Next, we recognize that the integral is in the form of an arcsin function, where the integral of is . Here, and . So, the integral becomes:
- Substitute Values: Now we check the answer choices to see which one matches our result.The correct answer is (B) .