AI tutor
Full solution
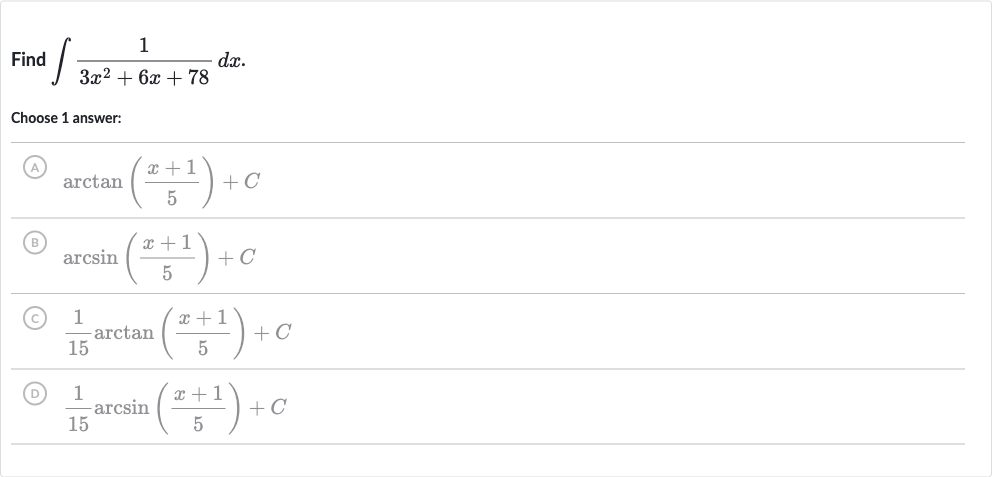
Q. Find .Choose answer:(A) (B) (c) (D)
- Complete the Square: First, let's complete the square for the quadratic in the denominator.Now, we need to add and subtract inside the parenthesis to complete the square.
- Rewrite with Completed Square: Now, we rewrite the integral with the completed square. Pull out the constant from the denominator.
- Apply Arctangent Integral Formula: Recognize that this is in the form of an arctangent integral.The integral of is , where is a constant.Here, , so .
- Integrate Using Arctangent Formula: Now, integrate using the arctangent formula.Simplify the constants.