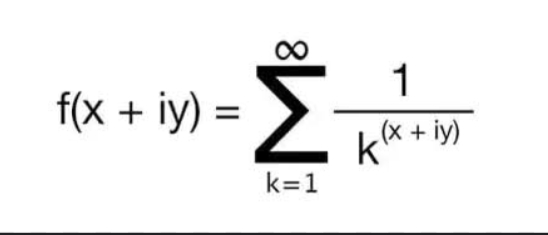AI tutor
Full solution
Q.
- Complex Exponents Properties: The given function is a complex series where each term is of the form . To evaluate this series, we need to understand the properties of complex exponents.
- Euler's Formula Application: The term can be rewritten using Euler's formula, which states that . Therefore, .
- General Term Expression: Now we can express the term as . This is the general term of the series .
- Dirichlet Series Convergence: The series is known as the Dirichlet series, which converges if the real part of the exponent, , is greater than . We need to ensure that x > 1 for the series to converge.
- Convergence Conditions: If x > 1, the series converges absolutely and uniformly on compact subsets of the half-plane \text{Re}(s) > 1, where . This is a condition for the convergence of the Dirichlet series.
- Series Evaluation Approach: Since the problem does not specify the value of , we cannot directly evaluate the series without knowing whether x > 1. If , the series may diverge or require a different approach to evaluate.
- Special Cases Consideration: Assuming x > 1, the series converges, but evaluating it to a closed-form expression is generally not possible except for special cases like the Riemann zeta function, where and is a positive integer greater than .
- Final Evaluation Conclusion: Without additional information on the value of and , we cannot provide a simplified exact answer for the series . The series is defined and converges for x > 1, but its evaluation is not straightforward.