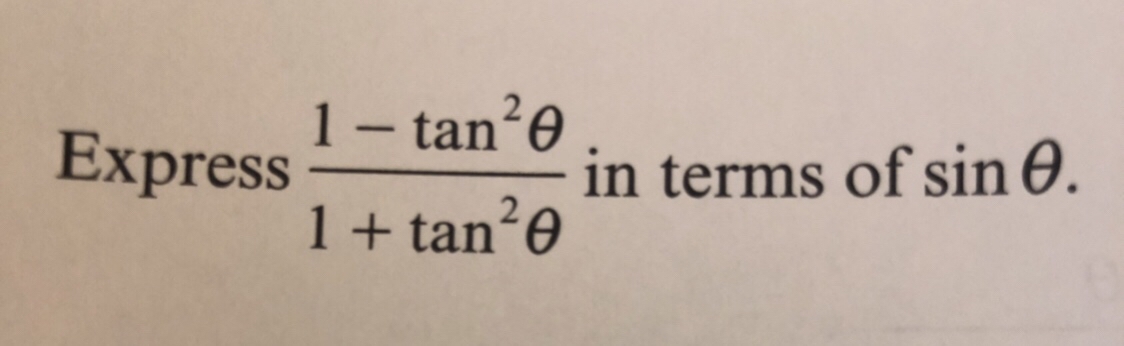AI tutor
Full solution
Q. Express in terms of .
- Rewrite using Pythagorean identity: Use the Pythagorean identity to rewrite the expression.
- Combine terms over common denominator: Combine the terms over a common denominator.=
- Recognize denominator identity: Recognize that the denominator is another Pythagorean identity: .
= - Simplify the expression: Simplify the expression.
- Express in terms of : Use the Pythagorean identity to express in terms of .=
- Combine like terms: Combine like terms.