Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of
log x,log y, and
log z.

log ((sqrt(x^(5)))/(z^(3)y^(2)))
Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x, \log y$ , and $\log z$ . $\newline$ $\log \frac{\sqrt{x^{5}}}{z^{3} y^{2}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Evaluate definite integrals using the power rule

Full solution

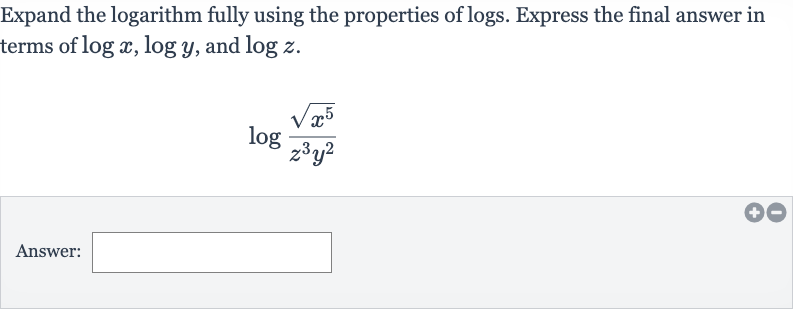
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x, \log y

, and

\log z

.

\newline

\log \frac{\sqrt{x^{5}}}{z^{3} y^{2}}

\newline

Answer:

Apply Quotient Rule: We start by applying the quotient rule of logarithms, which states that $\log(\frac{a}{b}) = \log(a) - \log(b)$ . In this case, we have $a = \sqrt{x^5}$ and $b = z^3y^2$ .
Apply Power Rule: Next, we apply the power rule of logarithms, which states that $\log(a^b) = b\cdot\log(a)$ . For the numerator, we have $\sqrt{x^5}$ which is $x^{5/2}$ , and for the denominator, we have $z^3$ and $y^2$ .
Rewrite Using Product Rule: We can now rewrite the logarithm as $\log(x^{\frac{5}{2}}) - (\log(z^3) + \log(y^2))$ by applying the product rule of logarithms, which states that $\log(ab) = \log(a) + \log(b)$ , to the denominator.
Apply Power Rule: We apply the power rule to each term: $\log(x^{\frac{5}{2}})$ becomes $\frac{5}{2}\cdot\log(x)$ , $\log(z^3)$ becomes $3\cdot\log(z)$ , and $\log(y^2)$ becomes $2\cdot\log(y)$ .
Subtract Logs: Subtracting the logs in the denominator from the log in the numerator, we get $(\frac{5}{2})\log(x) - 3\log(z) - 2\log(y)$ .
Final Expanded Form: This is the fully expanded form of the original logarithm in terms of $\log x$ , $\log y$ , and $\log z$ .

More problems from Evaluate definite integrals using the power rule

Question

Consider the following problem:

\newline

The water level under a bridge is changing at a rate of

r(t)=40 \sin \left(\frac{\pi t}{6}\right)

centimeters per hour (where

t

is the time in hours). At time

t=3

, the water level is

91

centimeters. By how much does the water level change during the

4^{\text {th }}

\newline

Which expression can we use to solve the problem?

\newline

1

\newline

\int_{3}^{4} r(t) d t

\newline

\int_{0}^{4} r(t) d t

\newline

\int_{4}^{5} r(t) d t

\newline

\int_{4}^{4} r(t) d t

Posted 1 month ago

Question

s(t)

gives the number of students enrolled in a school by time

t

\newline

\int_{15}^{18} s^{\prime}(t) d t=20

\newline

1

\newline

(A) The rate of change of enrollment is

20

students per year more in year

18

than it was in year

15

\newline

20

more students enrolled in year

18

15

\newline

(C) Between years

15

18

, the cumulative number of years of schooling of all of the enrolled students is

20

\newline

20

students enrolled in year

18

Posted 1 month ago

Question

A water tank is filled at a rate of

r(t)

liters per minute (where

t

is the time in minutes).

\newline

\int_{1}^{7} r^{\prime}(t) d t

\newline

1

\newline

(A) The rate at which the tank was filled at

t=7

\newline

B) The average rate of filling between

t=1

t=7

\newline

(C) The change in the rate of filling between

t=1

t=7

\newline

(D) The amount of water filled between

t=1

t=7

Posted 2 months ago

Question

The base of a solid is the region enclosed by the graphs of

y=\sin (x)

y=4-\sqrt{x}

x=2

x=7

\newline

Cross sections of the solid perpendicular to the

x

-axis are rectangles whose height is

2 x

\newline

Which one of the definite integrals gives the volume of the solid?

\newline

1

\newline

\int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x

\newline

\int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x

\newline

\int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x

\newline

\int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x

Posted 1 month ago

Question

Evaluate the integral.

\newline

\int-2 x^{3} \cos (3 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} 3^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} e^{4 x} d x

\newline

Posted 2 months ago

Question

\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}

Posted 2 months ago

Question

f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]

Posted 2 months ago

Question

\int \frac{1}{\cos(x)^{2}}\,dx

Posted 2 months ago