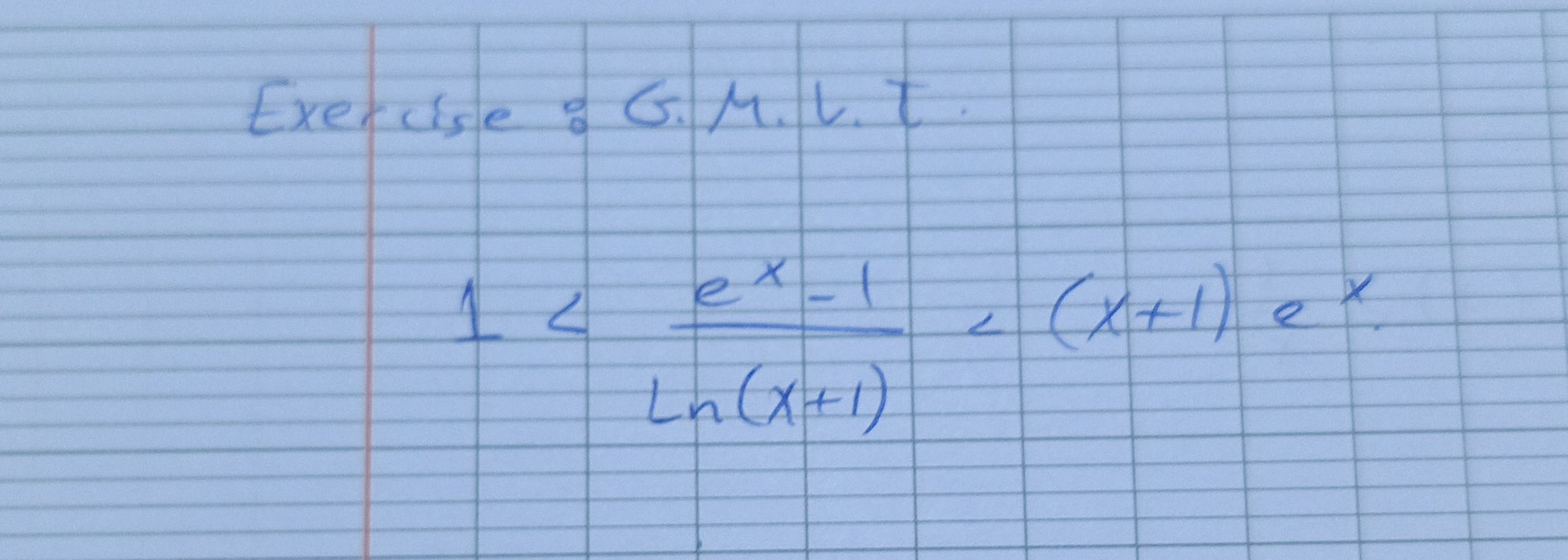Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Exercise: G.M.L.T.

1 < (e^(x)-1)/(ln(x+1)) < (x+1)e^(x)

Exercise: G.M.L.T. $\newline$ $1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}$

View step-by-step help

View step-by-step help

Solve advanced linear inequalities

Full solution

Q. Exercise: G.M.L.T.

\newline

1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}

Define Domain: First, we need to address the domain of the function $(e^{x}-1)/(\ln(x+1))$ to avoid any undefined expressions. The natural logarithm $\ln(x+1)$ is defined for $x > -1$ . Additionally, since we have an inequality involving a fraction, we must ensure that the denominator is not zero, so $x$ cannot be equal to $0$ . Thus, the domain of $x$ is $x > -1$ and $x \neq 0$ .
Solve Left Inequality: Next, we will solve the left part of the inequality: $1 < \frac{e^{x}-1}{\ln(x+1)}$ . We will multiply both sides by $\ln(x+1)$ to get rid of the denominator, but we must remember that the direction of the inequality will depend on the sign of $\ln(x+1)$ . Since $\ln(x+1)$ is positive for $x > 0$ and negative for $-1 < x < 0$ , we will have to consider these two cases separately.
Consider Cases: For $x > 0$ , $\ln(x+1)$ is positive. Multiplying both sides of the inequality by $\ln(x+1)$ gives us $\ln(x+1) < e^{x}-1$ . We then add $1$ to both sides to isolate $e^{x}$ on one side: $\ln(x+1) + 1 < e^{x}$ .
Solve Right Inequality: For $-1 < x < 0$ , $\ln(x+1)$ is negative. Multiplying both sides of the inequality by $\ln(x+1)$ and reversing the inequality sign gives us $\ln(x+1) > e^{x}-1$ . We then add $1$ to both sides to isolate $e^{x}$ on one side: $\ln(x+1) + 1 > e^{x}$ . However, this case leads to a contradiction since $e^{x}$ is always greater than $\ln(x+1) + 1$ for $-1 < x < 0$ . Therefore, there are no solutions in this interval.
Simplify Inequality: Now we will solve the right part of the inequality: $(e^{x}-1)/(\ln(x+1)) < (x+1)e^{x}$ . We will multiply both sides by $\ln(x+1)$ to get rid of the denominator. Since we are considering $x > 0$ , $\ln(x+1)$ is positive, and the direction of the inequality remains the same: $e^{x}-1 < (x+1)e^{x}\ln(x+1)$ .
Isolate Term: We simplify the inequality by distributing $e^{x}$ on the right side: $e^{x}-1 < e^{x}(x+1)\ln(x+1) - e^{x}\ln(x+1)$ . This simplifies to $-1 < e^{x}x\ln(x+1) - e^{x}\ln(x+1)$ .
Factor Out: We can then add $e^{x}\ln(x+1)$ to both sides to isolate the term with $x$ on one side: $e^{x}\ln(x+1) - 1 < e^{x}x\ln(x+1)$ .
Divide and Solve: Now we can factor out $e^{x}\ln(x+1)$ on the right side: $e^{x}\ln(x+1) - 1 < e^{x}\ln(x+1)(x)$ .
Complex Inequality: We divide both sides by $e^{x}\ln(x+1)$ to solve for $x$ . Since $e^{x}\ln(x+1)$ is positive for $x > 0$ , the direction of the inequality remains the same: $\frac{1}{e^{x}\ln(x+1)} - \frac{1}{(e^{x}\ln(x+1))^2} < x$ .
Summary: This inequality is quite complex to solve algebraically, and it may require numerical methods or graphing techniques to find the exact range of $x$ that satisfies it. However, we can see that as $x$ increases, the left side approaches $0$ , and thus for sufficiently large $x$ , the inequality will be satisfied.
Summary: This inequality is quite complex to solve algebraically, and it may require numerical methods or graphing techniques to find the exact range of $x$ that satisfies it. However, we can see that as $x$ increases, the left side approaches $0$ , and thus for sufficiently large $x$ , the inequality will be satisfied.To summarize, we have found that for $x > 0$ , the inequality $\ln(x+1) + 1 < e^{x}$ must be satisfied, and for sufficiently large $x$ , the inequality $\frac{1}{e^{x}\ln(x+1)} - \frac{1}{(e^{x}\ln(x+1))^2} < x$ is satisfied. Therefore, the range of $x$ that satisfies the original inequality is a subset of $x > 0$ , excluding any values that do not satisfy both parts of the inequality.

More problems from Solve advanced linear inequalities

Question

-2 x+b y=59

\newline

5 x-y=1

\newline

If the system of equations has exactly one solution

(x, y)

x=2

, what is the value of

b

Posted 2 months ago

Question

\newline

\frac{\sqrt[3]{2}}{\sqrt[3]{-128}}=

Posted 6 days ago

Question

\newline

\frac{\sqrt[4]{2}}{\sqrt[4]{162}}=

Posted 3 months ago

Question

\newline

\sqrt[5]{-16} \cdot 2^{\frac{1}{5}}=

Posted 2 months ago

Question

y

\newline

\begin{array}{l} \frac{y-1}{3 y+7}=\frac{1}{10} \\ y=\square \end{array}

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-30<\frac{x}{-4}

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-36+x<8

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

2 x<15

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

x-6 \leq 3

Posted 1 month ago

Question

x

\newline

Your answer must be simplified.

\newline

7>\frac{x}{4}

Posted 3 months ago