AI tutor
Full solution
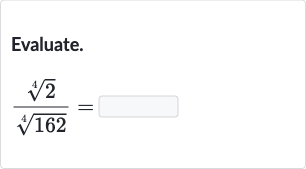
Q. Evaluate.
- Understanding the problem: First, let's understand the problem. We need to evaluate the expression which involves the fourth root of divided by the fourth root of .
- Combining the roots: We can simplify the expression by combining the roots since they have the same index (fourth root). The property of roots we use here is .
- Applying the property: Now, let's apply the property to our expression: .
- Simplifying the fraction: Next, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is . So, simplifies to .
- Rewriting the expression: Now we have . Since is , we can rewrite the expression as .
- Using the property of roots: Using the property of roots that .
- Final simplified value: Therefore, the final simplified value of the original expression is .
More problems from Solve advanced linear inequalities
QuestionGet tutor help