AI tutor
Full solution
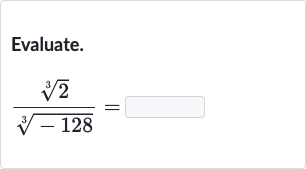
Q. Evaluate.
- Understand the problem: Understand the problem.We need to find the value of the cube root of divided by the cube root of .
- Apply cube root: Apply the cube root to both the numerator and the denominator.
- Simplify fraction: Simplify the fraction inside the cube root. can be simplified to because divided by is and we keep the negative sign.
- Evaluate cube root: Evaluate the cube root of . The cube root of is because . The cube root of is because . Therefore, .
More problems from Solve advanced linear inequalities
QuestionGet tutor help