AI tutor
Full solution
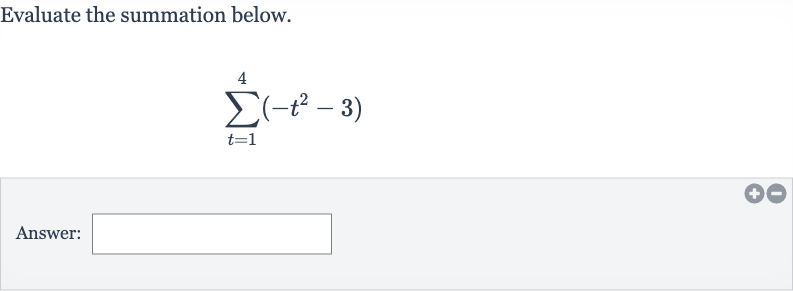
Q. Evaluate the summation below.Answer:
- Write and Evaluate for : Write down the summation expression and evaluate it for . The expression is . For , the expression becomes: .
- Evaluate for : Evaluate the expression for . For , the expression becomes: .
- Evaluate for : Evaluate the expression for . For , the expression becomes: .
- Evaluate for : Evaluate the expression for . For , the expression becomes: .
- Add and Sum: Add up the values obtained for , , , and .Sum = .
- Perform Addition: Perform the addition to find the total sum.Sum = .