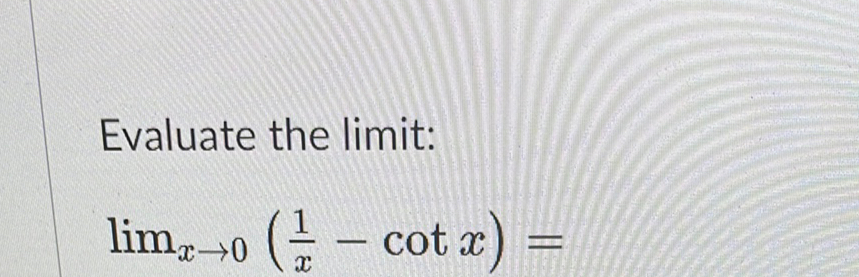AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the limit:
Full solution
Q. Evaluate the limit:
- Recognize singularity: We are given the limit to evaluate: First, we recognize that both and have singularities at , which means we need to find a way to combine these terms to eliminate the singularity. We can do this by finding a common denominator.
- Find common denominator: To find a common denominator, we need to express in terms of sine and cosine:Now we can rewrite the limit as:
- Combine fractions: The common denominator between and is . We multiply the numerator and denominator of by to get:
- Apply L'Hôpital's Rule: Now that we have a common denominator, we can combine the fractions:
- Differentiate numerator and denominator: We can now apply L'Hôpital's Rule because the limit is in an indeterminate form . We differentiate the numerator and the denominator with respect to :
Numerator's derivative:
Denominator's derivative: - Evaluate limit: We simplify the derivatives:Numerator's derivative simplifies to: Denominator's derivative is already simplified: Now we can rewrite the limit using these derivatives:
- Apply L'Hôpital's Rule again: We can now evaluate the limit by substituting into the simplified expression: However, this is still an indeterminate form, which means we need to apply L'Hôpital's Rule again.
- Differentiate second time: We differentiate the numerator and denominator again:Numerator's second derivative: Denominator's second derivative:
- Evaluate final limit: We simplify the second derivatives:Numerator's second derivative simplifies to: Denominator's second derivative simplifies to: Now we can rewrite the limit using these second derivatives:
- Evaluate final limit: We simplify the second derivatives:Numerator's second derivative simplifies to: Denominator's second derivative simplifies to: Now we can rewrite the limit using these second derivatives:We can now evaluate the limit by substituting into the second derivatives:
