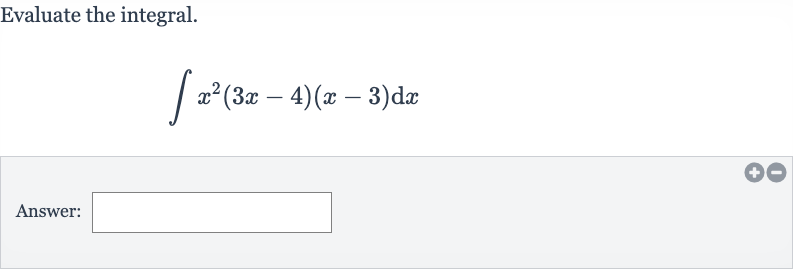AI tutor
Full solution
Q. Evaluate the integral.Answer:
- Expand Integrand: Expand the integrand to simplify the integral.We have the integral of a product of a quadratic and a linear term. We will first expand this product before integrating term by term.Now we can integrate each term separately.
- Integrate Expanded Polynomial: Integrate each term of the expanded polynomial separately.The integral of with respect to is , the integral of with respect to is , and the integral of with respect to is or .So, , where is the constant of integration.