Full solution
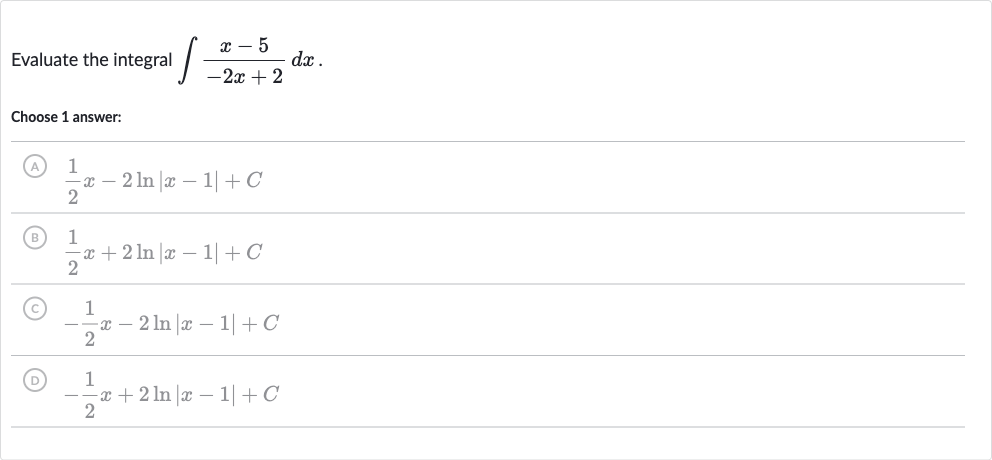
Q. Evaluate the integral .Choose answer:(A) (B) (C) (D)
- Rewrite Integral: Rewrite the integral as the sum of two simpler integrals.
- Split into Parts: Split the integral into two parts.
- Integrate First Part: Integrate the first part.
- Make Substitution: Make a substitution for the second part, let . , so
- Change Limits: Change the limits of integration according to the substitution.
- Integrate Second Part: Integrate the second part using the substitution.-\frac{\(5\)}{\(2\)} \int(\frac{\(1\)}{u})du = -\frac{\(5\)}{\(2\)} \ln|u| + C
- Substitute Back: Substitute back for \(u.
- Combine Integrals: Combine the two parts of the integral.
- Simplify Expression: Simplify the expression. (\frac{\(1\)}{\(2\)})x - \frac{\(5\)}{\(2\)} \ln|{\(-2\)x+\(2\)}| + C = (\frac{\(1\)}{\(2\)})x + (\frac{\(5\)}{\(2\)})\ln|x\(-1| + C