Full solution
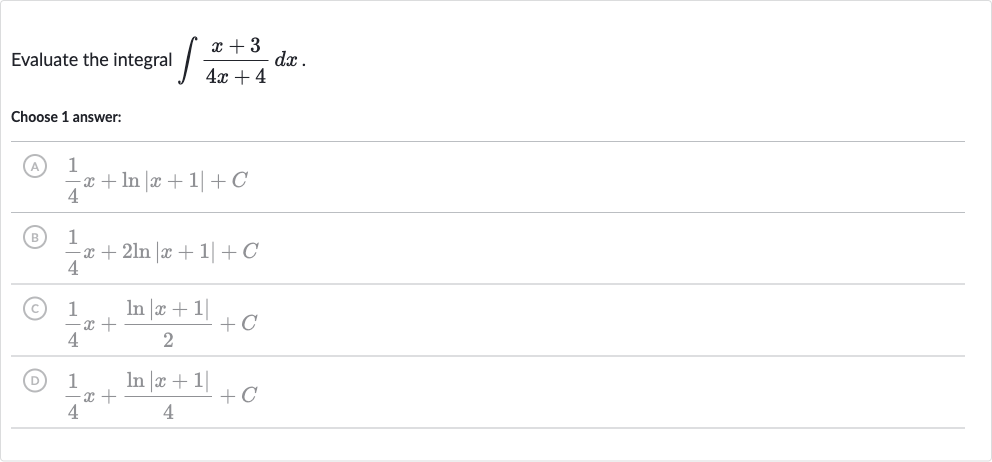
Q. Evaluate the integral .Choose answer:(A) (B) (C) (D)
- Split Integral: Now, split the integral into two parts.
- Substitution and Integration: For the first part, , we can use a simple substitution. Let , then and . Substitute into the integral. =
- Final Integration: Now, integrate both parts.
- Substitute Back: Substitute back for .= \frac{\(1\)}{\(4\)} x + \frac{\(1\)}{\(4\)} - \frac{\(1\)}{\(4\)} \ln|x+\(1| + C
- Combine Constants: Combine the constants into a single constant .