Full solution
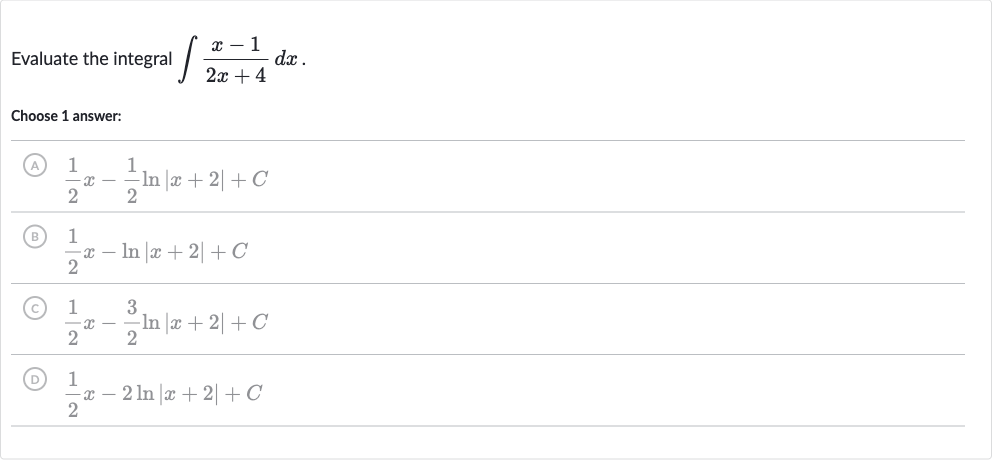
Q. Evaluate the integral .Choose answer:(A) (B) (C) (D)
- Split Integral: Let's split the integral into two parts by dividing each term in the numerator by the denominator.
- Integrate Parts: Now we integrate each part separately.and
- Use Natural Logarithm: To integrate , we use the natural logarithm.
- Combine Parts: Combine the two parts to get the final answer.
- Match Final Answer: Match the final answer with the given options.The correct answer is (A) .