Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral
int(3x+4)/(x+3)dx.
Choose 1 answer:
(A)
=9x-4ln |x+3|+C
(B)
=3x-5ln |x+3|+C
(C)
=3x+5ln |x+3|+C
(D)
=9x-5ln |x+3|+C

Evaluate the integral $\int \frac{3 x+4}{x+3} d x$ . $\newline$ Choose $1$ answer: $\newline$ (A) $=9 x-4 \ln |x+3|+C$ $\newline$ (B) $=3 x-5 \ln |x+3|+C$ $\newline$ (C) $=3 x+5 \ln |x+3|+C$ $\newline$ (D) $=9 x-5 \ln |x+3|+C$

View step-by-step help

View step-by-step help

Evaluate definite integrals using the chain rule

Full solution

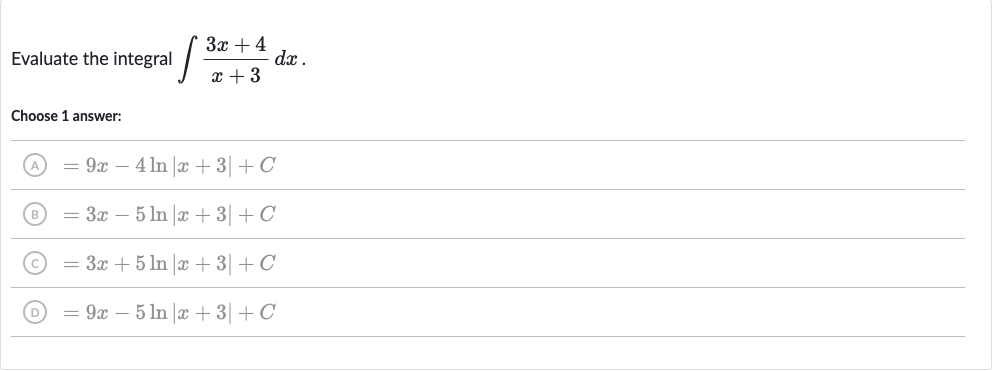
Q. Evaluate the integral

\int \frac{3 x+4}{x+3} d x

.

\newline

Choose

1

answer:

\newline

(A)

=9 x-4 \ln |x+3|+C

\newline

(B)

=3 x-5 \ln |x+3|+C

\newline

(C)

=3 x+5 \ln |x+3|+C

\newline

(D)

=9 x-5 \ln |x+3|+C

Simplify the integrand: First, let's try to simplify the integral by dividing the polynomial. We can rewrite the integrand as $3 + \left(\frac{1}{x+3}\right)$ .
Integrate each term: Now, we integrate each term separately. The integral of $3$ with respect to $x$ is $3x$ , and the integral of $\frac{1}{x+3}$ is $\ln|x+3|$ .
Finalize the integral: So, the integral becomes $3x + \ln|x+3| + C$ , where $C$ is the constant of integration.

More problems from Evaluate definite integrals using the chain rule

Question

The number of subscribers to a magazine is changing at a rate of

r(t)

subscribers per month (where

t

is time in months).

\newline

\int_{8}^{10} r^{\prime}(t) d t=7

\newline

1

\newline

(A) The rate of change of number of subscribers increased by

7

subscribers per month between

t=8

t=10

\newline

(B) As of month

10

, the magazine had

7

\newline

(C) The number of subscribers increased by

7

t=8

t=10

\newline

(D) The average rate of change in subscribers between month

8

10

7

subscribers per month.

Posted 9 months ago

Question

Consider the following problem:

\newline

The water level under a bridge is changing at a rate of

r(t)=40 \sin \left(\frac{\pi t}{6}\right)

centimeters per hour (where

t

is the time in hours). At time

t=3

, the water level is

91

centimeters. By how much does the water level change during the

4^{\text {th }}

\newline

Which expression can we use to solve the problem?

\newline

1

\newline

\int_{0}^{4} r(t) d t

\newline

\int_{4}^{5} r(t) d t

\newline

\int_{3}^{4} r(t) d t

\newline

\int_{4}^{4} r(t) d t

Posted 9 months ago

Question

The base of a solid is the region enclosed by the graphs of

y=\sin (x)

y=4-\sqrt{x}

x=2

x=7

\newline

Cross sections of the solid perpendicular to the

x

-axis are rectangles whose height is

2 x

\newline

Which one of the definite integrals gives the volume of the solid?

\newline

1

\newline

\int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x

\newline

\int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x

\newline

\int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x

\newline

\int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x

Posted 9 months ago

Question

\left(1\times\left(\left(\frac{1}{2}\right)^n-1\right)\right)\bigg/\left(\left(\frac{1}{2}\right)-1\right)

Posted 8 months ago

Question

\int \frac{1}{(x-2)(x^{2}+x+1)}\,dx

Posted 8 months ago

Question

What is the integral of the function

f(x) = \sin(2x)

\newline

\frac{-1}{2}\cos(x) + C

\newline

\frac{1}{2}\sin(x) + C

\newline

\frac{-1}{2}\cos(2x) + C

\newline

\frac{1}{2}\sin(2x) + C

Posted 8 months ago

Question

What is the integral of the function

\ f(x) = sin(2x)

\newline

\frac{-1}{2}\cos(x) + C

\newline

\frac{1}{2} \sin(x) + C

\newline

\frac{-1}{2}\cos(2x) + C

\newline

\frac{1}{2} \sin(2x) + c

Posted 8 months ago

Question

\int_{2}^{4} f(2x) \, dx = 10

\int_{4}^{8} f(u) \, du =

Posted 8 months ago

Question

\frac{d}{dt}\int_{2}^{t^{4}}e^{x^{2}}dx

Posted 8 months ago

Question

Evaluate and write the answer in scientific notation:

\newline

(1.48\times10^{3})(7\times10^{4})\div8.2\times10^{12}

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant