AI tutor
Full solution
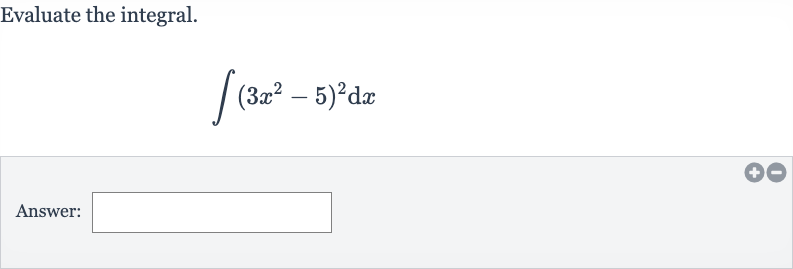
Q. Evaluate the integral.Answer:
- Expand the integrand: Expand the integrand . To integrate the function, we first need to expand the square of the binomial to simplify the integrand.
- Set up the integral: Set up the integral with the expanded form.Now we can write the integral as:
- Integrate each term separately: Integrate each term separately.The integral of a sum is the sum of the integrals, so we can integrate each term separately.
- Apply the power rule: Apply the power rule for integration to each term.The power rule states that , where is the constant of integration.
- Combine the integration results: Combine the results of the integrations.Now we combine the results from the previous step to get the antiderivative of the original function.
- Check for errors: Check for any mathematical errors. Review the steps to ensure that there are no mathematical errors in the calculations. No errors found.