Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral int(2x+1)/(x+2)dx. Choose 1 answer: (A) 2x-3ln |x+2|+C (B) ln |x+2|+C (C) x+ln |2x+1|+C (D) 2x-ln |x+2|+C

Evaluate the integral ∫2x+1x+2dx \int \frac{2 x+1}{x+2} d x .\newlineChoose 11 answer:\newline(A) 2x−3ln⁡∣x+2∣+C 2 x-3 \ln |x+2|+C \newline(B) ln⁡∣x+2∣+C \ln |x+2|+C \newline(C) x+ln⁡∣2x+1∣+C x+\ln |2 x+1|+C \newline(D) 2x−ln⁡∣x+2∣+C 2 x-\ln |x+2|+C

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

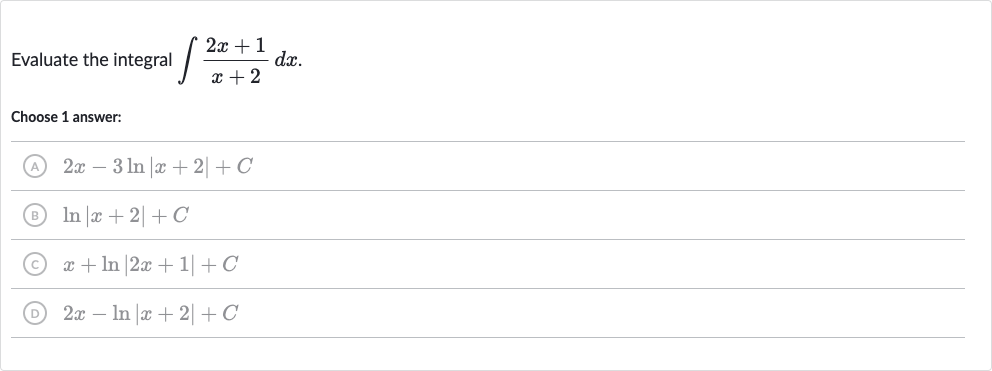
Q. Evaluate the integral ∫2x+1x+2dx \int \frac{2 x+1}{x+2} d x .\newlineChoose 11 answer:\newline(A) 2x−3ln⁡∣x+2∣+C 2 x-3 \ln |x+2|+C \newline(B) ln⁡∣x+2∣+C \ln |x+2|+C \newline(C) x+ln⁡∣2x+1∣+C x+\ln |2 x+1|+C \newline(D) 2x−ln⁡∣x+2∣+C 2 x-\ln |x+2|+C
  1. Divide and Simplify: Let's do long division first to simplify the integral.\newline(2x+1)/(x+2)(2x+1)/(x+2) can be divided to get 22 with a remainder of −3-3.\newlineSo, (2x+1)/(x+2)=2−3/(x+2)(2x+1)/(x+2) = 2 - 3/(x+2).
  2. Split Integral: Now we can split the integral into two parts. ∫2x+1x+2 dx=∫2 dx−∫3x+2 dx\int\frac{2x+1}{x+2}\,dx = \int 2 \,dx - \int \frac{3}{x+2} \,dx.
  3. Integrate Separately: Integrate each part separately.\newlineThe integral of 2 dx2 \, dx is 2x2x.\newlineThe integral of 3(x+2) dx\frac{3}{(x+2)} \, dx is 3ln⁡∣x+2∣3\ln|x+2|.
  4. Combine Integrals: Combine the two integrals.\newlineSo, ∫2x+1x+2 dx=2x−3ln⁡∣x+2∣+C\int \frac{2x+1}{x+2}\,dx = 2x - 3\ln|x+2| + C.
  5. Check Answer Choices: Check the answer choices.\newlineThe correct answer matches with (A) 2x−3ln⁡∣x+2∣+C2x - 3\ln|x+2| + C.

More problems from Evaluate definite integrals using the chain rule

Question
The number of subscribers to a magazine is changing at a rate of r(t) r(t) subscribers per month (where t t is time in months).\newlineWhat does ∫810r′(t)dt=7 \int_{8}^{10} r^{\prime}(t) d t=7 mean?\newlineChoose 11 answer:\newline(A) The rate of change of number of subscribers increased by 77 subscribers per month between t=8 t=8 and t=10 t=10 months.\newline(B) As of month 1010, the magazine had 77 subscribers.\newline(C) The number of subscribers increased by 77 between t=8 t=8 and t=10 t=10 months.\newline(D) The average rate of change in subscribers between month 88 and month 1010 was 77 subscribers per month.
Get tutor helpright-arrow

Posted 9 months ago

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(B) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(C) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 9 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(B) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(C) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x \newline(D) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x
Get tutor helpright-arrow

Posted 9 months ago

Question
(1×((12)n−1))/((12)−1)\left(1\times\left(\left(\frac{1}{2}\right)^n-1\right)\right)\bigg/\left(\left(\frac{1}{2}\right)-1\right)
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve∫1(x−2)(x2+x+1) dx\int \frac{1}{(x-2)(x^{2}+x+1)}\,dx.
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function f(x)=sin⁡(2x) f(x) = \sin(2x) ?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2}\sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+C \frac{1}{2}\sin(2x) + C
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the integral of the function  f(x)=sin(2x)\ f(x) = sin(2x)?\newline−12cos⁡(x)+C \frac{-1}{2}\cos(x) + C \newline12sin⁡(x)+C \frac{1}{2} \sin(x) + C \newline−12cos⁡(2x)+C \frac{-1}{2}\cos(2x) + C \newline12sin⁡(2x)+c \frac{1}{2} \sin(2x) + c
Get tutor helpright-arrow

Posted 8 months ago

Question
Suppose ∫24f(2x) dx=10 \int_{2}^{4} f(2x) \, dx = 10 . Then ∫48f(u) du= \int_{4}^{8} f(u) \, du =
Get tutor helpright-arrow

Posted 8 months ago

Question
Find ddt∫2t4ex2dx\frac{d}{dt}\int_{2}^{t^{4}}e^{x^{2}}dx
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate and write the answer in scientific notation: \newline(1.48×103)(7×104)÷8.2×1012(1.48\times10^{3})(7\times10^{4})\div8.2\times10^{12}
Get tutor helpright-arrow

Posted 8 months ago

View all (36)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant