Full solution
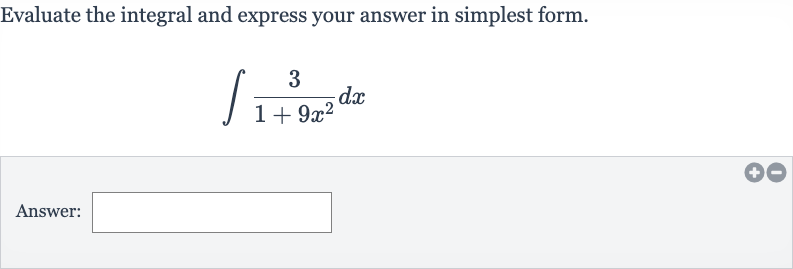
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Given Integral: We are given the integral to evaluate:To solve this integral, we can use a trigonometric substitution because the denominator has the form of , which suggests using the substitution .Let's choose , so that becomes .
- Trigonometric Substitution: First, we need to find in terms of . Differentiating with respect to gives us:
- Finding in terms of Now we substitute with and with in the integral:Simplify the integral using the trigonometric identity
- Substituting and in the integral: The terms cancel out, leaving us with: This integral is straightforward to evaluate:
- Simplifying the integral: Now we need to express back in terms of . From our substitution , we can write: So the integral becomes:
- Evaluating the integral: We have now found the antiderivative of the given function. The final answer in simplest form is: