Full solution
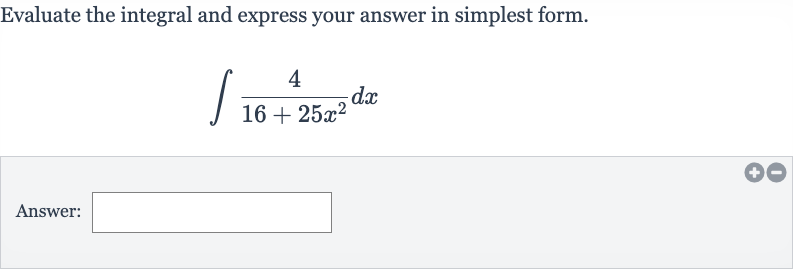
Q. Evaluate the integral and express your answer in simplest form.Answer:
- Recognize Trig Substitution: We are given the integral to evaluate: To simplify the integral, we can recognize that the denominator has the form of , where is a constant and is a function of . This suggests that we can use a trigonometric substitution, specifically the tangent substitution, where and . In our case, and , so and . Therefore, we can let , which gives us .
- Substitute and : Now we substitute and in the integral:Simplify the expression inside the integral:This simplifies to:Since , we can further simplify:
- Simplify Expression: We can now cancel out the terms and simplify the constants:This integral is straightforward to evaluate:
- Evaluate Integral: We now need to substitute back for using our original substitution . To find , we take the arctangent of both sides:So our integral in terms of is: