AI tutor
Full solution
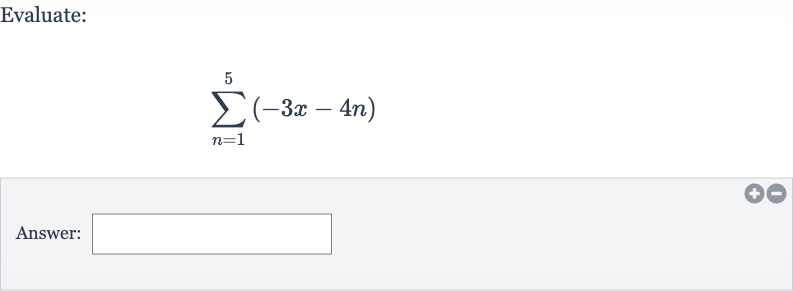
Q. Evaluate:Answer:
- Understand the problem: Understand the problem.We need to evaluate the sum of the expression for ranging from to . This is a finite arithmetic series where is the variable and is considered a constant within the context of the sum.
- Write out the terms: Write out the terms of the sum.The sum can be written out as:
- Simplify each term: Simplify each term in the sum.Now we simplify each term:
- Combine like terms: Combine like terms.We can combine the constant terms and the terms with :This simplifies to:
- Calculate sum of constants: Calculate the sum of the constant terms.Now we calculate the sum of the constant terms:
- Combine terms: Combine the terms with the sum of the constant terms.Now we combine the term with the sum of the constant terms:
- Write final answer: Write the final answer.The final answer is the expression we have obtained: