AI tutor
Full solution
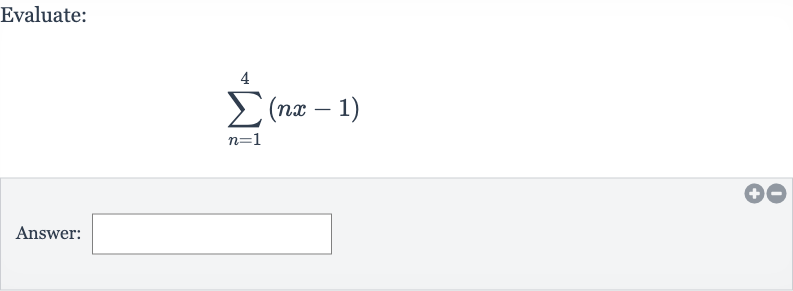
Q. Evaluate:Answer:
- Write Terms Explicitly: Write out the terms of the series explicitly.The series is , which means we add up the terms for each value of from to .So the terms are:
- Combine Like Terms: Combine like terms.We can combine the terms and the constant terms separately.This simplifies to:
- Check for Errors: Check for any mathematical errors.There are no mathematical errors in the previous steps. The terms were combined correctly, and the like terms were added together properly.
- Write Final Answer: Write the final answer.The sum of the series from to of the expression is .