Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate int_(6)^(e^(3)+5)(3x-16)/(x-5)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate ∫6e3+53x−16x−5dx \int_{6}^{e^{3}+5} \frac{3 x-16}{x-5} d x . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

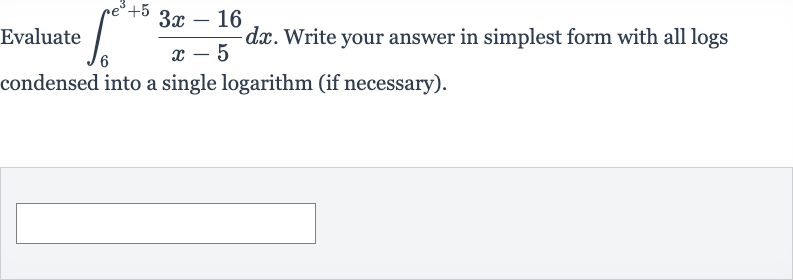
Q. Evaluate ∫6e3+53x−16x−5dx \int_{6}^{e^{3}+5} \frac{3 x-16}{x-5} d x . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).
  1. Rewrite Integral: We have the integral: \newline∫6e3+53x−16x−5 dx\int_{6}^{e^{3}+5}\frac{3x-16}{x-5}\,dx\newlineTo solve this integral, we will use the method of partial fractions. However, we notice that the numerator is already a degree less than the denominator, so we can proceed directly to integration.
  2. Integrate Constant Term: We can rewrite the integral as:\newline∫6e3+5(3−3⋅5−16x−5)dx\int_{6}^{e^{3}+5}(3 - \frac{3\cdot 5-16}{x-5})dx\newlineThis simplifies to:\newline∫6e3+5(3−1x−5)dx\int_{6}^{e^{3}+5}(3 - \frac{1}{x-5})dx\newlineNow we can integrate term by term.
  3. Integrate Fraction Term: The integral of the constant 33 is:\newline∫6e3+53dx=3x∣6e3+5\int_{6}^{e^{3}+5}3dx = 3x \bigg|_{6}^{e^{3}+5}\newlineEvaluating this from 66 to e3+5e^{3}+5 gives:\newline3(e3+5)−3(6)=3e3+15−18=3e3−33(e^{3}+5) - 3(6) = 3e^{3} + 15 - 18 = 3e^{3} - 3
  4. Combine Results: The integral of −1/(x−5)-1/(x-5) is:\newline∫6e3+5(−1x−5)dx=−ln⁡∣x−5∣∣6e3+5\int_{6}^{e^{3}+5}\left(-\frac{1}{x-5}\right)dx = -\ln|x-5| \bigg|_{6}^{e^{3}+5}\newlineEvaluating this from 66 to e3+5e^{3}+5 gives:\newline−ln⁡∣e3+5−5∣+ln⁡∣6−5∣=−ln⁡∣e3∣+ln⁡∣1∣=−3ln⁡(e)+ln⁡(1)-\ln|e^{3}+5-5| + \ln|6-5| = -\ln|e^{3}| + \ln|1| = -3\ln(e) + \ln(1)\newlineSince ln⁡(e)=1\ln(e) = 1 and ln⁡(1)=0\ln(1) = 0, this simplifies to:\newline−3(1)+0=−3-3(1) + 0 = -3
  5. Combine Results: The integral of −1/(x−5)-1/(x-5) is:\newline∫6e3+5(−1x−5)dx=−ln⁡∣x−5∣∣6e3+5\int_{6}^{e^{3}+5} \left(-\frac{1}{x-5}\right)dx = -\ln|x-5| \bigg|_{6}^{e^{3}+5}\newlineEvaluating this from 66 to e3+5e^{3}+5 gives:\newline−ln⁡∣e3+5−5∣+ln⁡∣6−5∣=−ln⁡∣e3∣+ln⁡∣1∣=−3ln⁡(e)+ln⁡(1)-\ln|e^{3}+5-5| + \ln|6-5| = -\ln|e^{3}| + \ln|1| = -3\ln(e) + \ln(1)\newlineSince ln⁡(e)=1\ln(e) = 1 and ln⁡(1)=0\ln(1) = 0, this simplifies to:\newline−3(1)+0=−3-3(1) + 0 = -3Combining the results from the two integrals, we get:\newline(3e3−3)−3=3e3−3−3=3e3−6(3e^{3} - 3) - 3 = 3e^{3} - 3 - 3 = 3e^{3} - 6\newlineThis is the final answer in its simplest form.

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant