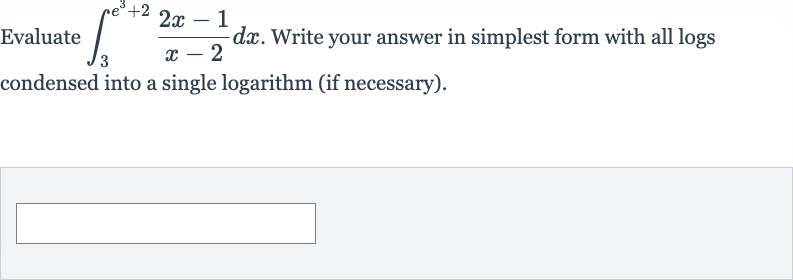
Evaluate int_(3)^(e^(3)+2)(2x-1)/(x-2)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(3)^(e^(3)+2)(2x-1)/(x-2)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Identify Integral Type: Identify the type of integral. We are dealing with an integral of a rational function, which suggests that we might need to use partial fraction decomposition. However, in this case, the numerator is a first-degree polynomial and the denominator is a first-degree polynomial as well, but not factorable. We can simplify the integral by dividing the numerator by the denominator.Perform Long Division: Perform long division for the integrand (2x-1)/(x-2). When we divide 2x by x, we get 2. Multiplying 2 by (x-2) gives us 2x-4. Subtracting this from 2x-1 gives us a remainder of 3. So, the integral can be rewritten as: ∫(2 + 3/(x-2)) dx from x=3 to x=e^(3)+2.Split into Two Integrals: Split the integral into two separate integrals. ∫(2 + 3/(x-2)) dx = ∫2 dx + ∫3/(x-2) dx. We can now integrate each term separately.Integrate Constant Term: Integrate the first term ∫2 dx. The integral of a constant is just the constant times the variable, so: ∫2 dx = 2x.Integrate Fraction Term: Integrate the second term ∫3/(x-2) dx. The integral of 1/(x-a) is ln|x-a|, so: ∫3/(x-2) dx = 3ln|x-2|.Combine Integral Results: Combine the results of the two integrals. The combined integral is: 2x + 3ln|x-2|.Evaluate Definite Integral: Evaluate the definite integral from x=3 to x=e^(3)+2. We substitute the upper and lower limits into the antiderivative: (2(e^(3)+2) + 3ln|e^(3)+2-2|) - (2(3) + 3ln|3-2|).Simplify Expression: Simplify the expression. 2(e^(3)+2) + 3ln(e^(3)) - 6 - 3ln(1) simplifies to: 2e^(3) + 4 + 3ln(e^(3)) - 6. Since ln(e^(3)) = 3 and ln(1) = 0, the expression further simplifies to: 2e^(3) + 4 + 9 - 6.Combine Like Terms: Combine like terms to get the final answer. 2e^(3) + 4 + 9 - 6 simplifies to: 2e^(3) + 7.

Evaluate $\int_{3}^{e^{3}+2} \frac{2 x-1}{x-2} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Evaluate ∫3e3+22x−1x−2dx \int_{3}^{e^{3}+2} \frac{2 x-1}{x-2} d x ∫3e3+2​x−22x−1​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{3}^{e^{3}+2} \frac{2 x-1}{x-2} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).