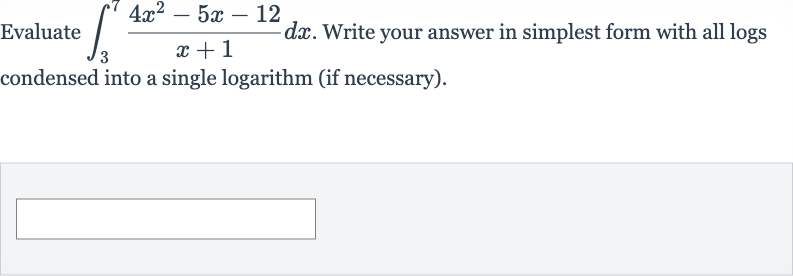
Evaluate int_(3)^(7)(4x^(2)-5x-12)/(x+1)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(3)^(7)(4x^(2)-5x-12)/(x+1)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Perform polynomial long division: Perform polynomial long division to simplify the integrand. We need to divide the polynomial 4x^2 - 5x - 12 by x + 1.Polynomial long division calculation: Polynomial long division calculation. (4x^2 - 5x - 12) ÷ (x + 1) = 4x - 9 - (3/(x + 1)) Now we can rewrite the integral as: ∫(3 to 7) (4x - 9 - 3/(x + 1)) dxSplit into three integrals: Split the integral into three separate integrals. ∫(3 to 7) (4x - 9 - 3/(x + 1)) dx = ∫(3 to 7) 4x dx - ∫(3 to 7) 9 dx - ∫(3 to 7) 3/(x + 1) dxEvaluate each integral separately: Evaluate each integral separately. First integral: ∫(3 to 7) 4x dx = 2x^2 | from x = 3 to x = 7 Second integral: ∫(3 to 7) 9 dx = 9x | from x = 3 to x = 7 Third integral: ∫(3 to 7) 3/(x + 1) dx = 3ln|x + 1| | from x = 3 to x = 7Calculate definite integrals: Calculate the definite integrals using the Fundamental Theorem of Calculus. First integral: 2x^2 | from x = 3 to x = 7 = 2(7^2) - 2(3^2) = 98 - 18 = 80 Second integral: 9x | from x = 3 to x = 7 = 9(7) - 9(3) = 63 - 27 = 36 Third integral: 3ln|x + 1| | from x = 3 to x = 7 = 3ln(7 + 1) - 3ln(3 + 1) = 3ln(8) - 3ln(4)Combine integral results: Combine the results from each integral. Total integral value = 80 - 36 - (3ln(8) - 3ln(4))Simplify the expression: Simplify the expression. Total integral value = 44 - 3ln(8) + 3ln(4) Since ln(a) - ln(b) = ln(a/b), we can combine the logarithms: Total integral value = 44 - 3ln(2^3/2^2) = 44 - 3ln(2)Write final answer: Write the final answer. The integral of (4x^2 - 5x - 12) / (x + 1) from x = 3 to x = 7 is 44 - 3ln(2).

Evaluate $\int_{3}^{7} \frac{4 x^{2}-5 x-12}{x+1} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Evaluate ∫374x2−5x−12x+1dx \int_{3}^{7} \frac{4 x^{2}-5 x-12}{x+1} d x ∫37​x+14x2−5x−12​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{3}^{7} \frac{4 x^{2}-5 x-12}{x+1} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).