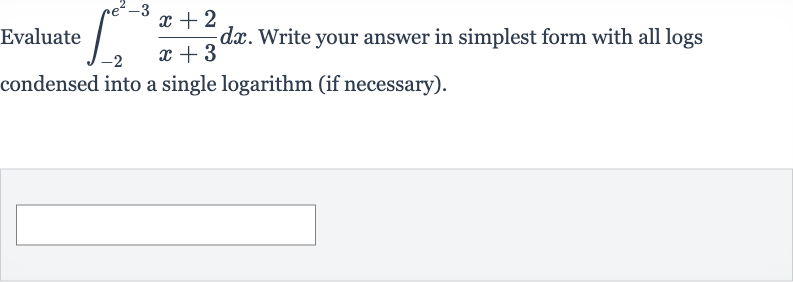
Evaluate int_(-2)^(e^(2)-3)(x+2)/(x+3)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(-2)^(e^(2)-3)(x+2)/(x+3)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Identify Integral: Identify the integral to be solved. We need to evaluate the integral of the function (x+2)/(x+3) within the limits of integration from x = -2 to x = e^(2)-3.Simplify Integrand: Simplify the integrand if possible. The integrand (x+2)/(x+3) can be rewritten as 1 + (-1)/(x+3) by dividing each term in the numerator by the denominator.Split Integral: Split the integral into two simpler integrals. The integral of the sum of two functions is the sum of their integrals. Therefore, we can write: ∫((x+2)/(x+3))dx = ∫(1)dx + ∫((-1)/(x+3))dxEvaluate First Integral: Evaluate the first integral. The integral of 1 with respect to x is x. So, ∫(1)dx = x.Evaluate Second Integral: Evaluate the second integral. The integral of (-1)/(x+3) with respect to x is -ln|x+3|. So, ∫((-1)/(x+3))dx = -ln|x+3|.Combine Results: Combine the results of the two integrals. The combined result of the integrals is x - ln|x+3|.Apply Limits: Apply the limits of integration. We need to evaluate (x - ln|x+3|) from x = -2 to x = e^(2)-3.Calculate Definite Integral: Calculate the definite integral. F(x) = x - ln|x+3| F(e^(2)-3) = (e^(2)-3) - ln|e^(2)-3+3| F(-2) = (-2) - ln|-2+3| Now, we subtract F(-2) from F(e^(2)-3): F(e^(2)-3) - F(-2) = (e^(2)-3) - ln|e^(2)| - [(-2) - ln|1|]Simplify Expression: Simplify the expression. Since ln|e^(2)| = 2 and ln|1| = 0, we have: (e^(2)-3) - 2 - [(-2) - 0] = e^(2)-3 - 2 + 2 = e^(2)-3Write Final Answer: Write the final answer. The final value of the integral is e^(2)-3.

Evaluate $\int_{-2}^{e^{2}-3} \frac{x+2}{x+3} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Evaluate ∫−2e2−3x+2x+3dx \int_{-2}^{e^{2}-3} \frac{x+2}{x+3} d x ∫−2e2−3​x+3x+2​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{-2}^{e^{2}-3} \frac{x+2}{x+3} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).