Full solution

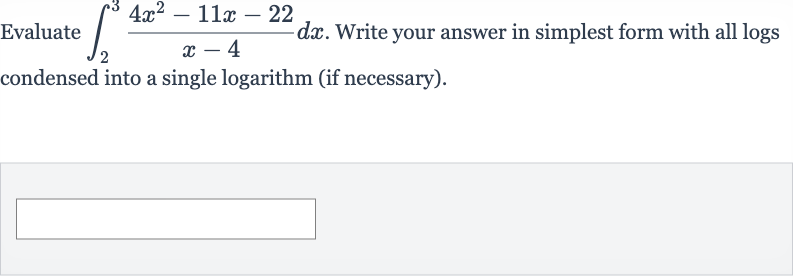
Q. Evaluate

\int_{2}^{3} \frac{4 x^{2}-11 x-22}{x-4} d x

. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Perform Long Division: First, we need to perform polynomial long division to simplify the integrand $(4x^2 - 11x - 22) / (x - 4)$ . This will allow us to integrate the function more easily.
Simplify Numerator: Performing the long division, we divide $4x^2$ by $x$ to get $4x$ . Multiplying $(x - 4)$ by $4x$ gives us $4x^2 - 16x$ . We subtract this from the original numerator to get a new numerator of $5x - 22$ .
Integrate Each Term: Continuing the long division, we divide $5x$ by $x$ to get $5$ . Multiplying $(x - 4)$ by $5$ gives us $5x - 20$ . We subtract this from the new numerator to get a remainder of $-2$ .
Evaluate Definite Integral: The result of the long division is that $(4x^2 - 11x - 22) / (x - 4)$ simplifies to $4x + 5 - \frac{2}{x - 4}$ . Now we can integrate each term separately.
Calculate Values: The integral of $4x$ with respect to $x$ is $2x^2$ , the integral of $5$ with respect to $x$ is $5x$ , and the integral of $-2/(x - 4)$ with respect to $x$ is $-2\ln|x - 4|$ . So the integral of our function from $2$ to $x$ $0$ is the integral of $x$ $1$ from $2$ to $x$ $0$ .
Sum Up Results: We evaluate the definite integral by calculating the antiderivative at the upper limit and subtracting the antiderivative at the lower limit. For $2x^2$ , we get $2(3)^2 - 2(2)^2$ . For $5x$ , we get $5(3) - 5(2)$ . For $-2\ln|x - 4|$ , we get $-2\ln|3 - 4| - (-2\ln|2 - 4|)$ .
Sum Up Results: We evaluate the definite integral by calculating the antiderivative at the upper limit and subtracting the antiderivative at the lower limit. For $2x^2$ , we get $2(3)^2 - 2(2)^2$ . For $5x$ , we get $5(3) - 5(2)$ . For $-2\ln|x - 4|$ , we get $-2\ln|3 - 4| - (-2\ln|2 - 4|)$ .Calculating the values, we get $2(9) - 2(4)$ for the first term, which is $18 - 8$ . For the second term, we get $15 - 10$ . For the third term, we get $-2\ln|-1| - (-2\ln|-2|)$ , which simplifies to $2(3)^2 - 2(2)^2$ $0$ since the absolute value of a negative number is positive and $2(3)^2 - 2(2)^2$ $1$ is $2(3)^2 - 2(2)^2$ $2$ .
Sum Up Results: We evaluate the definite integral by calculating the antiderivative at the upper limit and subtracting the antiderivative at the lower limit. For $2x^2$ , we get $2(3)^2 - 2(2)^2$ . For $5x$ , we get $5(3) - 5(2)$ . For $-2\ln|x - 4|$ , we get $-2\ln|3 - 4| - (-2\ln|2 - 4|)$ .Calculating the values, we get $2(9) - 2(4)$ for the first term, which is $18 - 8$ . For the second term, we get $15 - 10$ . For the third term, we get $-2\ln|-1| - (-2\ln|-2|)$ , which simplifies to $2(3)^2 - 2(2)^2$ $0$ since the absolute value of a negative number is positive and $2(3)^2 - 2(2)^2$ $1$ is $2(3)^2 - 2(2)^2$ $2$ .Adding up the values, we get $2(3)^2 - 2(2)^2$ $3$ . This simplifies to $2(3)^2 - 2(2)^2$ $4$ , which is $2(3)^2 - 2(2)^2$ $5$ .