Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate
int_(11)^(e^(3)+10)(2x-19)/(x-10)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{11}^{e^{3}+10} \frac{2 x-19}{x-10} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

View step-by-step help

View step-by-step help

Evaluate definite integrals using the chain rule

Full solution

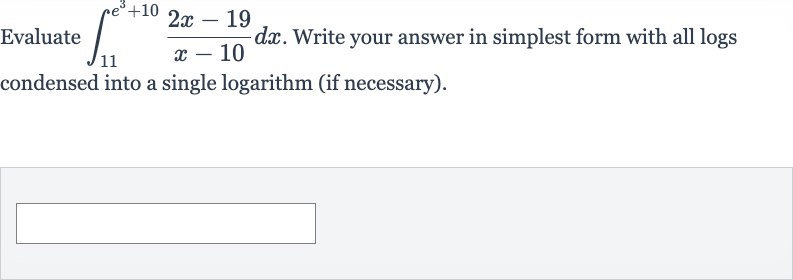
Q. Evaluate

\int_{11}^{e^{3}+10} \frac{2 x-19}{x-10} d x

. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Simplify: Simplify the integrand if possible. $\newline$ The integrand $(2x-19)/(x-10)$ can be simplified by long division since the degree of the numerator is equal to the degree of the denominator. We divide $2x$ by $x$ to get $2$ and multiply $(x-10)$ by $2$ to get $2x-20$ . We then subtract this from the numerator to get a remainder of $1$ . So, the integrand simplifies to $2 + 1/(x-10)$ .
Break down: Break the integral into two simpler integrals. $\newline$ We can write the integral as the sum of two simpler integrals: $\newline$ $\int\frac{2x-19}{x-10} dx = \int 2 dx + \int\frac{1}{x-10} dx$
Integrate separately: Integrate each term separately. $\newline$ The integral of $2$ with respect to $x$ is $2x$ , and the integral of $1/(x-10)$ with respect to $x$ is $\ln|x-10|$ . So we have: $\newline$ $\int 2 \, dx = 2x$ $\newline$ $\int \frac{1}{(x-10)} \, dx = \ln|x-10|$
Combine and evaluate: Combine the antiderivatives and evaluate the definite integral. $\newline$ The combined antiderivative is $2x + \ln|x-10|$ . We need to evaluate this from $11$ to $e^{3}+10$ : $\newline$ $(2x + \ln|x-10|)$ evaluated from $11$ to $e^{3}+10$ is: $\newline$ $(2(e^{3}+10) + \ln|e^{3}+10-10|) - (2(11) + \ln|11-10|)$
Simplify expression: Simplify the expression. $\newline$ Now we plug in the limits of integration: $\newline$ $= (2(e^{3}+10) + \ln|e^{3}|) - (22 + \ln|1|)$ $\newline$ $= (2e^{3} + 20 + \ln(e^{3})) - (22 + \ln(1))$ $\newline$ Since $\ln(e^{3}) = 3$ and $\ln(1) = 0$ , we can further simplify: $\newline$ $= (2e^{3} + 20 + 3) - (22 + 0)$ $\newline$ $= 2e^{3} + 23 - 22$ $\newline$ $= 2e^{3} + 1$

More problems from Evaluate definite integrals using the chain rule

Question

Consider the following problem:

\newline

The water level under a bridge is changing at a rate of

r(t)=40 \sin \left(\frac{\pi t}{6}\right)

centimeters per hour (where

t

is the time in hours). At time

t=3

, the water level is

91

centimeters. By how much does the water level change during the

4^{\text {th }}

\newline

Which expression can we use to solve the problem?

\newline

1

\newline

\int_{3}^{4} r(t) d t

\newline

\int_{0}^{4} r(t) d t

\newline

\int_{4}^{5} r(t) d t

\newline

\int_{4}^{4} r(t) d t

Posted 1 year ago

Question

s(t)

gives the number of students enrolled in a school by time

t

\newline

\int_{15}^{18} s^{\prime}(t) d t=20

\newline

1

\newline

(A) The rate of change of enrollment is

20

students per year more in year

18

than it was in year

15

\newline

20

more students enrolled in year

18

15

\newline

(C) Between years

15

18

, the cumulative number of years of schooling of all of the enrolled students is

20

\newline

20

students enrolled in year

18

Posted 1 year ago

Question

A water tank is filled at a rate of

r(t)

liters per minute (where

t

is the time in minutes).

\newline

\int_{1}^{7} r^{\prime}(t) d t

\newline

1

\newline

(A) The rate at which the tank was filled at

t=7

\newline

B) The average rate of filling between

t=1

t=7

\newline

(C) The change in the rate of filling between

t=1

t=7

\newline

(D) The amount of water filled between

t=1

t=7

Posted 1 year ago

Question

The base of a solid is the region enclosed by the graphs of

y=\sin (x)

y=4-\sqrt{x}

x=2

x=7

\newline

Cross sections of the solid perpendicular to the

x

-axis are rectangles whose height is

2 x

\newline

Which one of the definite integrals gives the volume of the solid?

\newline

1

\newline

\int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x

\newline

\int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x

\newline

\int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x

\newline

\int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x

Posted 1 year ago

Question

Evaluate the integral.

\newline

\int-2 x^{3} \cos (3 x) d x

\newline

Posted 1 year ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} 3^{3 x} d x

\newline

Posted 1 year ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} e^{4 x} d x

\newline

Posted 1 year ago

Question

\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}

Posted 1 year ago

Question

f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]

Posted 1 year ago

Question

\int \frac{1}{\cos(x)^{2}}\,dx

Posted 1 year ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant