Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

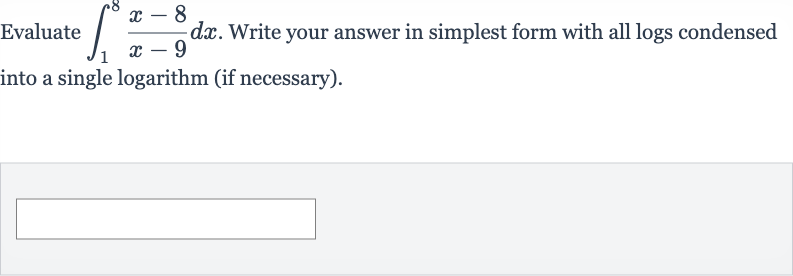
Evaluate
int_(1)^(8)(x-8)/(x-9)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{1}^{8} \frac{x-8}{x-9} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

View step-by-step help

View step-by-step help

Evaluate definite integrals using the chain rule

Full solution

Q. Evaluate

\int_{1}^{8} \frac{x-8}{x-9} d x

. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate Integral: We need to evaluate the integral of the function $(x-8)/(x-9)$ from $1$ to $8$ . To do this, we will first perform a partial fraction decomposition if possible. However, in this case, the numerator is of lower degree than the denominator, and the fraction is already simplified, so we can proceed to integrate directly.
Rewrite Integral: Let's rewrite the integral by splitting the fraction into two parts: $\newline$ $\int_{1}^{8}\frac{x-8}{x-9}\,dx = \int_{1}^{8}(1 + \frac{-1}{x-9})\,dx$ $\newline$ This is done by dividing $x-9$ into $x-8$ , which gives us $1$ with a remainder of $-1$ .
Integrate Separately: Now we can integrate each part separately: $\newline$ $\int_{1}^{8}(1 + (-1)/(x-9))\,dx = \int_{1}^{8}\,dx + \int_{1}^{8}(-1/(x-9))\,dx$ $\newline$ The first integral is straightforward, and the second integral is a standard logarithmic integral.
Evaluate First Integral: Evaluating the first integral gives us: $\int_{1}^{8}\mathrm{d}x = x \bigg|_{1}^{8} = 8 - 1 = 7$
Evaluate Second Integral: Evaluating the second integral gives us: $\newline$ $\int_{1}^{8}\left(-\frac{1}{x-9}\right)dx = -\ln|x-9| \bigg|_{1}^{8}$ $\newline$ We will evaluate this at the bounds $1$ and $8$ .
Evaluate Logarithmic Part: Plugging in the bounds for the logarithmic part, we get: $\newline$ $-\ln|8-9| + \ln|1-9| = -\ln|-1| + \ln|-8| = -\ln(1) + \ln(8)$ $\newline$ Since the natural logarithm of $1$ is $0$ , this simplifies to: $\newline$ $-\ln(1) + \ln(8) = \ln(8)$
Combine Results: Combining the results from the two integrals, we get: $\newline$ $7 - \ln(1) + \ln(8) = 7 + \ln(8)$ $\newline$ This is the final answer, and it is already in the simplest form with a single logarithm.

More problems from Evaluate definite integrals using the chain rule

Question

Consider the following problem:

\newline

The water level under a bridge is changing at a rate of

r(t)=40 \sin \left(\frac{\pi t}{6}\right)

centimeters per hour (where

t

is the time in hours). At time

t=3

, the water level is

91

centimeters. By how much does the water level change during the

4^{\text {th }}

\newline

Which expression can we use to solve the problem?

\newline

1

\newline

\int_{3}^{4} r(t) d t

\newline

\int_{0}^{4} r(t) d t

\newline

\int_{4}^{5} r(t) d t

\newline

\int_{4}^{4} r(t) d t

Posted 8 months ago

Question

s(t)

gives the number of students enrolled in a school by time

t

\newline

\int_{15}^{18} s^{\prime}(t) d t=20

\newline

1

\newline

(A) The rate of change of enrollment is

20

students per year more in year

18

than it was in year

15

\newline

20

more students enrolled in year

18

15

\newline

(C) Between years

15

18

, the cumulative number of years of schooling of all of the enrolled students is

20

\newline

20

students enrolled in year

18

Posted 7 months ago

Question

A water tank is filled at a rate of

r(t)

liters per minute (where

t

is the time in minutes).

\newline

\int_{1}^{7} r^{\prime}(t) d t

\newline

1

\newline

(A) The rate at which the tank was filled at

t=7

\newline

B) The average rate of filling between

t=1

t=7

\newline

(C) The change in the rate of filling between

t=1

t=7

\newline

(D) The amount of water filled between

t=1

t=7

Posted 8 months ago

Question

The base of a solid is the region enclosed by the graphs of

y=\sin (x)

y=4-\sqrt{x}

x=2

x=7

\newline

Cross sections of the solid perpendicular to the

x

-axis are rectangles whose height is

2 x

\newline

Which one of the definite integrals gives the volume of the solid?

\newline

1

\newline

\int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x

\newline

\int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x

\newline

\int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x

\newline

\int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x

Posted 8 months ago

Question

Evaluate the integral.

\newline

\int-2 x^{3} \cos (3 x) d x

\newline

Posted 9 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} 3^{3 x} d x

\newline

Posted 9 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} e^{4 x} d x

\newline

Posted 9 months ago

Question

\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}

Posted 8 months ago

Question

f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]

Posted 8 months ago

Question

\int \frac{1}{\cos(x)^{2}}\,dx

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant