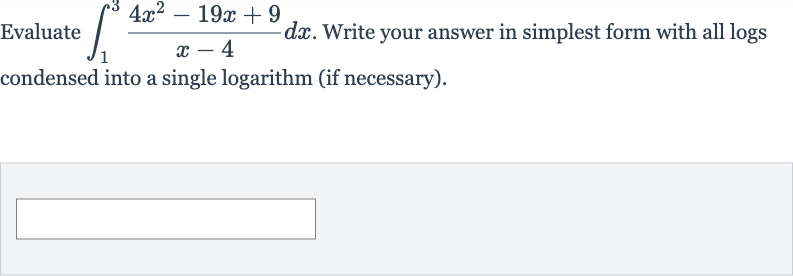
Evaluate int_(1)^(3)(4x^(2)-19 x+9)/(x-4)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Question

Evaluate  int_(1)^(3)(4x^(2)-19 x+9)/(x-4)dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Bytelearn · Accepted Answer

Perform Polynomial Long Division: First, we will perform polynomial long division to simplify the integrand (4x^2 - 19x + 9)/(x - 4). Dividing 4x^2 by x gives us 4x. Multiplying 4x by (x - 4) gives us 4x^2 - 16x. Subtracting this from the original numerator, we get -19x + 9 - (4x^2 - 16x) = -3x + 9. Dividing -3x by x gives us -3. Multiplying -3 by (x - 4) gives us -3x + 12. Subtracting this from the previous remainder, we get 9 - (-3x + 12) = 3x - 3. Since 3x - 3 is of lower degree than the divisor x - 4, we stop here. The result of the division is 4x - 3 with a remainder of 3x - 3. So, the integrand can be rewritten as 4x - 3 + (3x - 3)/(x - 4).Split Integral into Two Parts: Now, we can split the integral into two parts: ∫(4x - 3)dx from 1 to 3 and ∫(3x - 3)/(x - 4)dx from 1 to 3. The first integral is straightforward to evaluate: ∫(4x - 3)dx = 2x^2 - 3x + C. Evaluating from 1 to 3 gives us (2(3)^2 - 3(3)) - (2(1)^2 - 3(1)) = (18 - 9) - (2 - 3) = 9 + 1 = 10.Evaluate First Integral: The second integral ∫(3x - 3)/(x - 4)dx from 1 to 3 is more complex. We can rewrite the numerator to match the derivative of the denominator: Let's rewrite 3x - 3 as 3(x - 4) + 12, so the integral becomes ∫(3(x - 4) + 12)/(x - 4)dx. This can be split into two integrals: 3∫(x - 4)/(x - 4)dx + 12∫1/(x - 4)dx. The first part simplifies to 3∫1dx, which is just 3x. The second part is 12∫1/(x - 4)dx, which is 12ln|x - 4| + C.Rewrite Numerator for Second Integral: Now we can evaluate the second integral from 1 to 3: 3∫1dx from 1 to 3 is simply 3x evaluated from 1 to 3, which gives us 3(3) - 3(1) = 9 - 3 = 6. 12∫1/(x - 4)dx from 1 to 3 is 12ln|x - 4| evaluated from 1 to 3, which gives us 12ln|3 - 4| - 12ln|1 - 4| = 12ln|-1| - 12ln|-3| = 12ln(1) - 12ln(3). Since ln(1) is 0, this simplifies to -12ln(3).Evaluate Second Integral: Combining the results from the two parts of the integral, we have: The integral from 1 to 3 of (4x^2 - 19x + 9)/(x - 4)dx is equal to 10 (from the first part) plus 6 (from the second part, the 3x term) minus 12ln(3) (from the second part, the logarithmic term). So, the final answer is 16 - 12ln(3).

Evaluate $\int_{1}^{3} \frac{4 x^{2}-19 x+9}{x-4} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Evaluate ∫134x2−19x+9x−4dx \int_{1}^{3} \frac{4 x^{2}-19 x+9}{x-4} d x ∫13​x−44x2−19x+9​dx. Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).

Evaluate $\int_{1}^{3} \frac{4 x^{2}-19 x+9}{x-4} d x$ . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).