AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).
Full solution
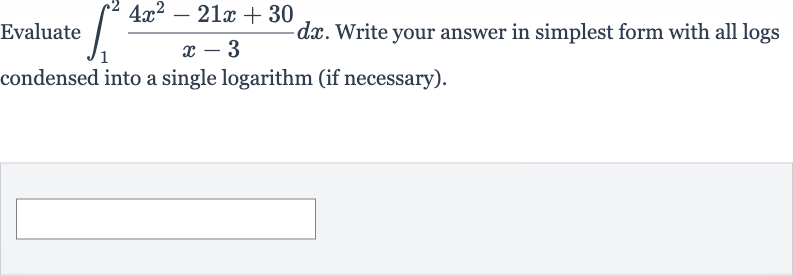
Q. Evaluate . Write your answer in simplest form with all logs condensed into a single logarithm (if necessary).
- Perform Polynomial Long Division: Perform polynomial long division to simplify the integrand.We need to divide the polynomial by .
- Polynomial Long Division Calculation: Polynomial long division calculation. with a remainder of .So, .
- Set Up Integral: Set up the integral with the simplified integrand. .
- Integrate Each Term: Integrate each term separately.The integral of is , the integral of is , and the integral of is $\(-3\)\ln|x - \(3\)|.
- Calculate Definite Integral: Calculate the definite integral from \(1\) to \(2\).
\[\int_{1}^{2}(4x + 3)\,dx = [2x^2 + 3x]_1^2 = (2(2)^2 + 3(2)) - (2(1)^2 + 3(1)),\]
\[\int_{1}^{2}\left(\frac{3}{x - 3}\right)dx = [-3\ln|x - 3|]_1^2 = -3\ln|2 - 3| + 3\ln|1 - 3|.\] - Perform Calculations: Perform the calculations for each part.\(\newline\)For the polynomial part: \((2(2)^2 + 3(2)) - (2(1)^2 + 3(1)) = (8 + 6) - (2 + 3) = 14 - 5 = 9\).\(\newline\)For the logarithmic part: \(-3\ln|2 - 3| + 3\ln|1 - 3| = -3\ln|-1| + 3\ln|-2| = -3\ln(1) + 3\ln(2) = 3\ln(2)\).
- Combine Results: Combine the results to get the final answer.\(\newline\)The final answer is the sum of the polynomial part and the logarithmic part: \(9 + 3\ln(2)\).
