Full solution
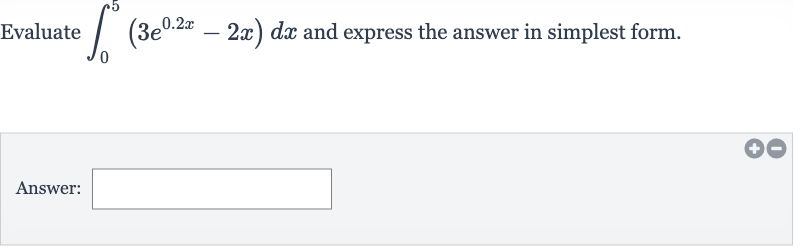
Q. Evaluate and express the answer in simplest form.Answer:
- Identify Terms: Identify the two separate terms in the integral.We have the integral of the sum of two functions: and . We can integrate each term separately.
- Integrate : Integrate the first term .To integrate , we use the fact that the integral of is , where is a constant.So, the integral of is .
- Integrate : Integrate the second term . The integral of with respect to is .
- Combine Integrals: Combine the integrals of the two terms.The integral of the function is .
- Evaluate Definite Integral: Evaluate the definite integral from to . We need to calculate evaluated at and subtract the value of the function evaluated at . At : . At : .
- Subtract Values: Subtract the value at the lower limit from the value at the upper limit..