Full solution
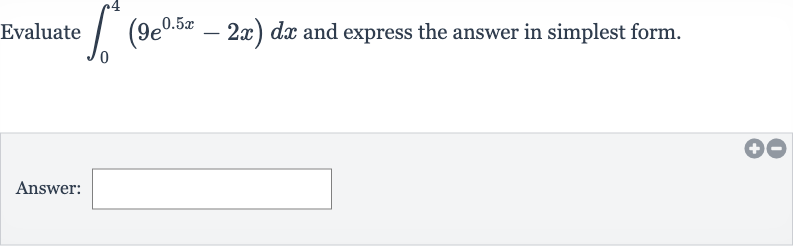
Q. Evaluate and express the answer in simplest form.Answer:
- Evaluate Definite Integral: Now we evaluate the definite integral from to .We calculate the value of the antiderivative at the upper limit of integration (x = ):
- Calculate Upper Limit: Next, we calculate the value of the antiderivative at the lower limit of integration (x = ):
- Calculate Lower Limit: We subtract the value of the antiderivative at the lower limit from the value at the upper limit to find the definite integral: