Full solution
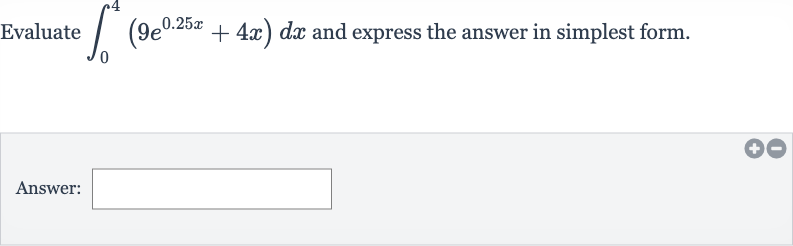
Q. Evaluate and express the answer in simplest form.Answer:
- Identify Integral: Identify the integral to be solved.We need to evaluate the integral of the function with respect to from to .
- Break into Two: Break the integral into two separate integrals.The integral of a sum is the sum of the integrals, so we can write:
- Evaluate First Integral: Evaluate the first integral . To integrate , we can use the substitution method: Let , then , or . The integral becomes: The integral of is , so we have: Substituting back for , we get:
- Evaluate Second Integral: Evaluate the second integral . The integral of with respect to is , so we have:
- Combine Results: Combine the results of the two integrals.The combined indefinite integral is:
- Evaluate Definite Integral: Evaluate the definite integral from to . We need to calculate the value of the combined integral at the upper limit () and subtract the value at the lower limit (). For : For : Now subtract the value at from the value at :
- Write Final Answer: Write the final answer.The value of the definite integral from to is .