Full solution
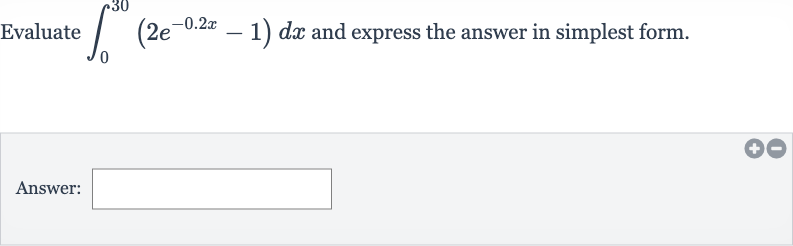
Q. Evaluate and express the answer in simplest form.Answer:
- Break down the integral: Break down the integral into two separate integrals. \int_{\(0\)}^{\(30\)}(\(2e^{.x} - )\,dx = \int_{}^{}e^{.x}\,dx - \int_{}^{}\,dx
- Evaluate first integral: Evaluate the first integral . Let , then , which implies . The limits of integration change from to to to . The integral becomes .
- Evaluate integral of : Evaluate the integral of .
So, - Evaluate second integral: Evaluate the second integral . This is a simple integral, which results in evaluated from to .
- Combine results: Combine the results from Step and Step .Simplify the expression.
- Calculate exact value: Calculate the exact value of the expression.= = =