Full solution
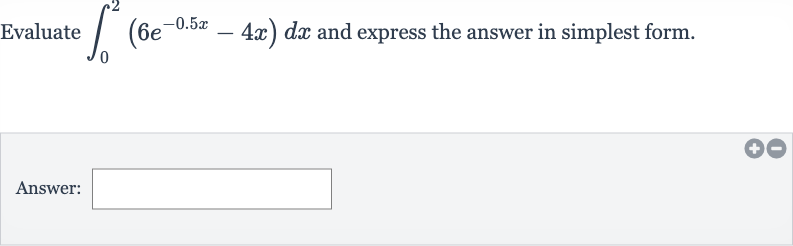
Q. Evaluate and express the answer in simplest form.Answer:
- Break down into two integrals: Break down the integral into two separate integrals.
- Evaluate integral of : Evaluate the first integral . Let , then , which implies . When , , and when , . The integral becomes .
- Calculate integral of : Calculate the integral of . The integral of with respect to is . So, .
- Evaluate integral of : Evaluate the second integral . The integral of with respect to is . So, .
- Combine results from Step and Step : Combine the results from Step and Step . The result of the integral from to of the function is .
- Simplify the expression: Simplify the expression. .