Full solution
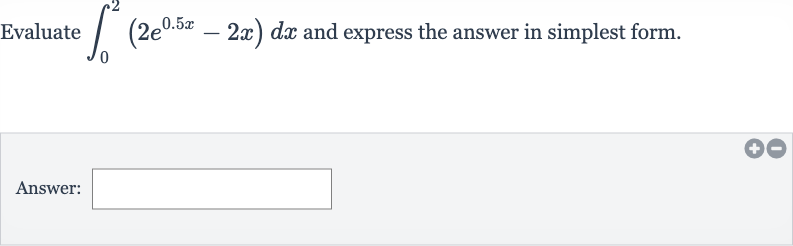
Q. Evaluate and express the answer in simplest form.Answer:
- Identify Integral: Identify the integral to be solved.We need to evaluate the integral of the function from to . This integral can be split into two separate integrals:
- Evaluate First Integral: Evaluate the first integral.The first integral is . To solve this, we can use the substitution method or recognize that the antiderivative of is . Here, , so the antiderivative is . Therefore, the integral becomes: from to Evaluating this at the bounds gives us:
- Evaluate Second Integral: Evaluate the second integral.The second integral is . The antiderivative of is , so the antiderivative of is . Therefore, the integral becomes: from to Evaluating this at the bounds gives us:= = =
- Combine Results: Combine the results from Step and Step .Now we combine the results of the two integrals to get the final answer: