Full solution
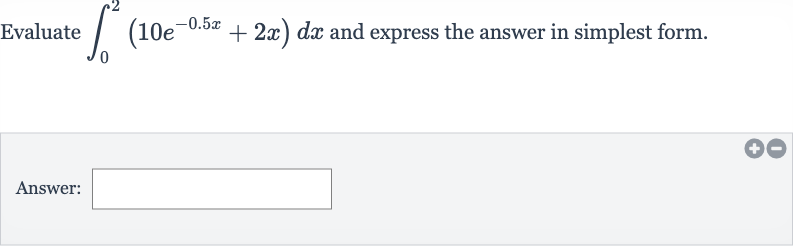
Q. Evaluate and express the answer in simplest form.Answer:
- Identify Terms: Identify the two separate terms in the integral.We have the integral of two terms: and . We will integrate each term separately.
- Integrate First Term: Integrate the first term . The integral of with respect to is , so the integral of is . Calculation:
- Integrate Second Term: Integrate the second term . The integral of with respect to is , so the integral of is . Calculation:
- Combine Integrals: Combine the results of the two integrals.The combined indefinite integral is .
- Evaluate Definite Integral: Evaluate the definite integral from to . We need to calculate evaluated at and subtract the value of the function evaluated at . Calculation:
- Perform Evaluation: Perform the evaluation and simplification.Calculation: [(-20e^{-1} + 4) - (-20e^{0} + 0)]\(\newlineCalculation: \$[(-20/e + 4) - (-20\cdot 1 + 0)]\(\newline\)Calculation: \$[-20/e + 4 + 20]\(\newline\)Calculation: \$24 - 20/e\)
- Write Final Answer: Write the final answer in simplest form.\(\newline\)The final answer is \(24 - \frac{20}{e}\).