Full solution
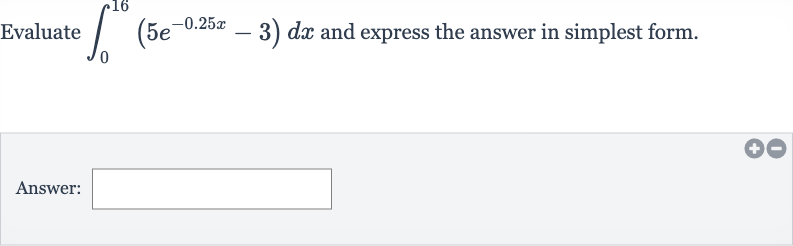
Q. Evaluate and express the answer in simplest form.Answer:
- Break down into two integrals: Break down the integral into two separate integrals.
- Evaluate first integral: Evaluate the first integral . Let , then , which implies . The limits of integration change from to to to . The integral becomes .
- Evaluate integral of : Evaluate the integral of .
So, - Evaluate second integral: Evaluate the second integral . This is a simple integral, and the result is evaluated from to . So, .
- Combine results: Combine the results from Step and Step .
- Simplify expression: Simplify the expression.