AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate and express the answer in simplest form.Answer:
Full solution
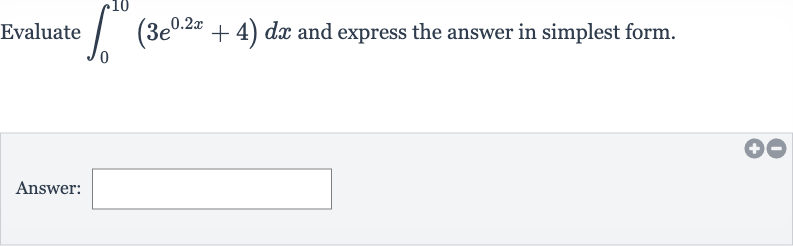
Q. Evaluate and express the answer in simplest form.Answer:
- Identify Integral: Identify the integral to be solved.We need to evaluate the integral of the function with respect to , from the lower limit of to the upper limit of .
- Break into Two: Break the integral into two separate integrals.The integral of a sum is the sum of the integrals, so we can write:\int(\(3e^{.x} + )\,dx = \int e^{.x}\,dx + \int \,dx
- Evaluate First Integral: Evaluate the first integral . To integrate , we recognize that the derivative of is , so we need to divide by to compensate for the chain rule when taking the antiderivative: \int \(3e^{(.x)}\,dx = \left(\frac{}{.}\right)\int e^{(.x)}(.\,dx) = \int e^{(.x)}\,d(.x) = e^{(.x)} + C
- Evaluate Second Integral: Evaluate the second integral . The antiderivative of a constant is just the constant times the variable of integration:
- Combine Results: Combine the results of Step and Step .The combined indefinite integral is:
- Apply Fundamental Theorem: Apply the Fundamental Theorem of Calculus to evaluate the definite integral from to . We need to evaluate the combined expression at the upper limit of and subtract the evaluation at the lower limit of :
- Perform Calculations: Perform the calculations for the upper and lower limits.For the upper limit :For the lower limit :
- Subtract Lower Limit: Subtract the lower limit evaluation from the upper limit evaluation.
- Simplify Final Answer: Simplify the final answer.The final answer is .
