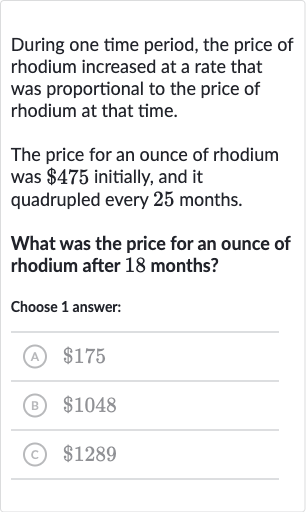
During one time period, the price of rhodium increased at a rate that was proportional to the price of rhodium at that time. The price for an ounce of rhodium was $475 initially, and it quadrupled every 25 months. What was the price for an ounce of rhodium after 18 months? Choose 1 answer: (A) $175 (B) $1048 (C) $1289

Question

During one time period, the price of rhodium increased at a rate that was proportional to the price of rhodium at that time. The price for an ounce of rhodium was  $475 initially, and it quadrupled every 25 months. What was the price for an ounce of rhodium after 18 months? Choose 1 answer: (A)  $175 (B)  $1048 (C)  $1289

Bytelearn · Accepted Answer

Understand the problem: First, we need to understand the problem. We are given that the price of rhodium quadruples every 25 months. This means that every 25 months, the price is 4 times what it was at the beginning of the period.Calculate growth rate: To find the price after 18 months, we need to determine the rate of growth per month. Since the price quadruples every 25 months, we can use the formula for exponential growth: Final Price = Initial Price * (Growth Rate)^(Time Period).Find monthly growth rate: We know that the price quadruples (which is a 4-fold increase) every 25 months. To find the monthly growth rate, we can take the fourth root of 4, because 4^(1/25) will give us the growth rate that, when applied 25 times, results in a quadrupling of the price. Growth Rate = 4^(1/25)Calculate growth rate: Now we calculate the growth rate using the fourth root of 4. Growth Rate = 4^(1/25) ≈ 1.0567 (rounded to four decimal places for simplicity)Apply growth rate to initial price: Next, we apply this growth rate to the initial price of $475 over the 18-month period. Final Price = Initial Price * (Growth Rate)^(Time Period) Final Price = $475 * (1.0567)^18Calculate final price: We calculate the final price using the growth rate and the time period of 18 months. Final Price ≈ $475 * (1.0567)^18 ≈ $475 * 2.2182 ≈ $1053.645 (rounded to the nearest dollar)Choose closest option: Looking at the answer choices, we see that $1053.645 is closest to $1048, which is option (B).

Full solution

More problems from Percent of change: word problems

Related topics